WaBis
walter.bislins.ch
Analytische Lösung für die erste Bifurkationsstelle im Feigenbaumdiagramm
Auf dieser Seite befasse ich mich mit einem Problem aus der Chaosforschung. Die Chaosforschung (auch: Theorie komplexer Systeme oder Komplexitätstheorie) ist ein Teilgebiet der Mathematik und Physik und befasst sich im Wesentlichen mit dynamischen Systemen, deren Dynamik unter bestimmten Bedingungen empfindlich von den Anfangsbedingungen abhängt, sodass ihr Verhalten nicht langfristig vorhersagbar ist. Da diese Dynamik einerseits den physikalischen Gesetzen unterliegt, andererseits aber irregulär erscheint, bezeichnet man sie als deterministisches Chaos. Chaotische dynamische Systeme sind nichtlinear.
Mathematisches Modell
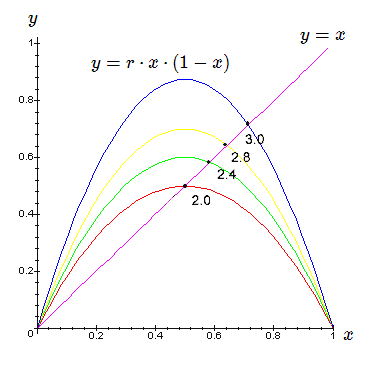
Eine sehr einfache nichtlineare Formel stellt (1) dar. Es handelt sich um eine in x quadratische Formel.
| (1) |
| ||||||
| wobei' |
|
Hinweis: Eine leicht erweiterte Form dieser Formel habe ich unter Lösung für erste Bifurkationsstelle (Übung2) durchgerechnet.
Wenn man mit einem beliebigen Startwert x0 zwischen 0 und 1 beginnt und diesen Wert für xn einsetzt, erhält man als Resultat einen neuen Wert xn+1. Wenn man diesen neuen Wert wieder in der Formel rechts einsetzt, erhält man einen weiteren Wert usw.
Bei verschiedenen r können die folgenden Verhaltensweisen für grosse n beobachtet werden. Dabei hängt dieses Verhalten nicht vom Anfangswert ab, sondern nur von r:
- Mit r von 0 bis 1 erhält man immer 0 nach einigen Iterationen.
- Mit r zwischen 1 und 3 stellt sich ein bestimmter Grenzwert ein. Diese Grenzwerte nennt man Attraktoren (siehe Diagramm).
- Mit r zwischen 3 und 1 + √6 (etwa 3,45) wechselt die Folge bei fast allen Startwerten (ausgenommen 0, 1 und 1−1/r, siehe Anmerkung) zwischen zwei Attraktoren.
- Mit r zwischen 1 + √6 und ungefähr 3,54 wechselt die Folge bei fast allen Startwerten zwischen vier Attraktoren (siehe Anmerkung).
- Wird r grösser als 3,54, stellen sich erst 8, dann 16, 32 usw. Attraktoren ein.
- Bei r annähernd 3,57 beginnt das Chaos.
Dieser Übergang von konvergentem Verhalten über Periodenverdopplungen zu chaotischen Verhalten ist generell für nichtlineare Systeme typisch, die in Abhängigkeit von einem Parameter r chaotisches oder nicht chaotisches Verhalten zeigen. Die Übergänge zur Periodenverdoppelung nennt man Bifurkationspunkte.
Anmerkung
Für Werte von r zwischen 3 und 1 + √6 konvergieren die meisten x Werte zu einem der angegebenen Attraktoren. Als Ausnahme wurden die Werte x = 0, 1 und x = 1−1/r angegeben. Eigentlich gibt es noch mehr Ausnahmen, nämlich alle Werte x0, welche nach n Iterationen den Wert xn = 1−1/r ergeben.
Der erste Startwert, der diese Bedingung erfüllt, ist x0 = 1/r, denn x1 = xn = 1−1/r.
Der zweite Startwert, der diese Bedingung erfüllt, ist x0 = 1/2 ± √1/4−1/r2, denn dann wird x1 = 1/r und x2 = xn = 1−1/r.
Es gibt noch mehr solcher spezielle Startwerte. Siehe dazu Spezielle Startwerte ( Feigenbaum-Diagramm erzeugen und analysieren).
Feigenbaum-Diagramm erzeugen und analysieren).
Berechnung des ersten Attraktors
Bis zur ersten Bifurkationsstelle konvergieren alle xn Werte gegen eine bestimmte von r abhängige Zahl x(r), Attraktor genannt. Das bedeutet, wenn man xn = x(r) in die Formel (1) einsetzt, erhält man für xn+1 = x(r), also wieder exakt dieselbe Zahl:
| (2) |
P1 |
Das Polynom auf der rechten Seite des Gleichheitszeichens von (2) nenne ich P1. Die Grafik rechts zeigt die linke und die rechte Seite der Gleichung (2). Die linke Seite y = x stellt eine 45 Grad Gerade dar. Die rechte Seite der Gleichung jeweils eine Parabel P1 dar, welche je nach Wert von r unterschiedlich aussieht. Gezeigt werden hier 4 Parabeln für Werte von r zwischen 2 und 3.
Dort wo sich die Parabel mit der Geraden schneidet ist die Lösung für die Gleichung (2), denn dort ist die linke Seite der Gleichung gleich der rechten Seite.
Um nun die Schnittpunkte der Parabel mit der Geraden zu berechnen, also den Wert des Attraktors als Funktion von r, formt man die Gleichung (2) so um, dass alle x auf einer Seite sind und sucht die Nullstellen des Polynoms:
Gleichung (2) ausmultiplizieren und alle x auf eine Seite:
| (3) |
Man sieht, dass eine Lösung x = 0 ist (für x Null eingesetzt erfüllt die Gleichung):
| (4) |
|
Lösung nicht interessant |
Diese Lösung ist nicht interessant. Sie entspricht dem Schnittpunkt der Parabel mit der Geraden im Nullpunkt.
Wir können die Gleichung (3) durch x dividieren und die erhaltene lineare Gleichung nach x auflösen. Damit erhalten wir die zweite Lösung, welche dem Wert des Attraktors als Funktion von r entspricht:
| (5) |
|
Erster Attraktor |
Wenn für r zwischen 1 und 3 der Wert xn = xb in die Formel (1) eingesetzt wird, erhalten wir wieder exakt diesen Wert xn+1 = xb. Werden andere Werte für xn eingesetzt, so nähern sie sich bei jedem Durchgang dem Wert xb immer mehr. Daher nennt man diesen Wert: Attraktor (Anzieher).
Im Fall der Periodenverdopplung existiert dieser auf sich selbst abbildende Punkt zwar immer noch, aber er stellt keinen Attraktor mehr dar. Die Iteration der Gleichung (1) konvergiert für r > 3 nicht mehr gegen xb.
Berechnung der ersten Bifurkationsstelle
Die Werte r, an denen sich das Feigenbaumdiagramm aufteilt, werden Bifurkationsstellen genannt. Die erste Bifurkationsstelle kann relativ einfach noch analytisch berechnet werden. Das Vorgehen dazu ist wiefolgt:
- Gleichung für 2 Attraktoren aufstellen. Dies ergibt ein Polynom 4. Grades, P2 in der Grafik.
- Die zwei bereits bekannten Lösungen xa und xb verwenden, um das Polynom P2 auf den Grad 2 zu reduzieren.
- Lösen des Polynoms 2. Grades aus Schritt 2.
- Dort wo sich die Lösungen von Schritt 3. treffen, ist die Stelle der ersten Bifurkation: r1.
1. Gleichung für 2 Attraktoren
Wir betrachten nun den Bereich des Feigenbaumdiagrammes, wo für jedes r die Werte zwischen zwei Attraktoren wechseln. Dies bedeutet nichts anderes, als dass die Formel (1) zweimal hintereinander ausgeführt wieder denselben Wert ergeben muss. Also zum Beispiel der Wert xc in (1) eingesetzt ergibt xd, und xd ergibt wieder xc usw. (siehe (6) und (7)).
| (6) | |
| (7) | |
| (8) |
Wir können also Formel (7) und (8) in (6) einsetzen und erhalten:
| (9) |
Ausmultipliziert und nach Potenzen gruppiert erhalten wir das Polynom 4. Grades P2, welches in der Grafik oben rechts in rot eingezeichnet ist:
| (10) |
|
Polynom P2 |
Die vier Schnittpunkte von P2 mit der Geraden P0 interessieren uns nun. Zwei der Schnittpunkte xa und xb kennen wir bereits von der Berechnung des ersten Attraktors (Schnitt von P1 mit P0).
2. Polynom P2 auf Grad 2 reduzieren
Um die Schnittpunkte zu berechnen, müssen wir bei der Formel (10) alle x auf die gleiche Seite bringen und das Ganze = 0 setzen:
| (11) |
Wir müssen jetzt die Nullstellen dieses Polynoms bestimmen. Da wir aber bereits die 2 Lösungen xa und xb kennen, können wir durch diese Nullstellen dividieren, womit sich das Polynom 4. Grades auf ein Polynom 2. Grades reduziert.
Durch Nullstellen dividiert man, indem man im Nenner ein Polynom aus diesen Nullstellen erstellt nach dem Muster:
| (12) |
Die Polynomdivision sieht dann folgendermassen aus:
| (13) |
Das Dividieren von Polynomen ist eine sehr fehlerträchtige Angelegenheit und recht aufwändig. Wenn man keine Fehler gemacht hat, müsste das Dividieren ohne Rest aufgehen. Man erhält das folgende Polynom 2. Grades:
| (14) |
|
3. Lösen des Polynoms 2. Grades
Durch Lösen dieser quadratischen Gleichung erhalten wir die Werte der zwei Attraktoren xc und xd:
| (15) |
|
Alternierende Attraktoren |
4. Bifurkationsstelle berechnen
Wir müssen nun jenen Wert von r berechnen, an dem die zwei Attraktoren xc und xd aus (15) zusammentreffen, also denselben Wert haben. Dies ist dann der Fall, wenn der Wert unter der Wurzel von (15) gleich Null ist, denn dann ist der ± Term gleich 0 und damit haben beide Lösungen der Gleichung denselben Wert:
| (16) |
Jetzt müssen wir nur diese quadratische Gleichung nach r lösen:
| (17) |
|
Da r in unserem Diagramm immer positiv sein muss, kommt nur die Lösung r1 = 3 in Frage.
Resultat
Die berechnete Bifurkationsstelle liegt also bei:
| (18) |
|
Beachte, dass für r = 3 die Formel (5) für den ersten Attraktor genau denselben Wert ergibt, wie Formel (15) für die beiden alternierenden Attraktoren, da sich an diesem Punkt die 3 Attraktoren treffen.
Kommentare
in Gleichung (8) fehlt bei dem letzten x ein Quadrat. Das fehlt auch in der darauf folgenden Gleichung (9). In Gleichung (10) stimmt es wieder.
Mit freundlichen Grüßen,
Juliane Klamser
@Juliane Klamser
Sie haben vollkommen recht! Vielen Dank für Ihre Aufmerksamkeit und das Melden des Fehlers. Ich habe die beiden Formeln korrigiert.
Liebe Grüsse, Walter Bislin
In der Aussage: "Mit r zwischen 3 und 1 + √6 (etwa 3,45) wechselt die Folge bei fast allen Startwerten (ausgenommen 0, 1 und 1-1/r) zwischen zwei Attraktoren." sind mit 0, 1 und 1-1/r nicht alle Ausnahmen abgedeckt: 1/r beispielsweise wird auf 1-1/r abgebildet, das anschließend immer wieder auf sich selbst abgebildet wird. 1/2+√(1/4-1/r^2) und 1/2-√(1/4-1/r^2) werden wiederum auf zuvor genanntes 1/r abgebildet und landen somit langfristig auch auf 1-1/r. Das kann man beliebig fortsetzten: Wenn man die Gleichung x'=r*x*(1-x) nach x auflöst, sieht man für jedes x'<r/4 zwei x findet, die auf x' abgebildet werden und von denen für min. eins gilt: x<1/2<r/4, sodass man zu diesem wieder neue Startwerte findet, die auf es abgebildet werden.
Damit gibt es unendlich viele Ausnahmen.
@Dennis Reichard
Du hast recht. Ich habe einen entsprechenden Kommentar unter Anmerkung eingefügt. Weitere Informationen findest Du auch unter Spezielle Startwerte ( Feigenbaum-Diagramm erzeugen und analysieren).
Feigenbaum-Diagramm erzeugen und analysieren).
Vielen Dank für Deinen Hinweis.
- Name wird bei deinem Kommentar angezeigt.
- Email ist nur für den Administrator, sie wird nicht angezeigt.
- Du kannst deine Kommentare eine Zeit lang editieren oder löschen.
- Du kannst Formatierungen im Kommentar verwenden, z.B: Code, Formeln, usw.
- Externen Links und Bilder werden nicht angezeigt, bis sie der Admin freischaltet.