WaBis
walter.bislins.ch
Flat-Earth: Wie stark ist die Krümmung der Erde?
Mit Hilfe einer interaktiven Simulation zeige ich, bis in welche Höhen die Erde flach erscheint, obwohl sie tatsächlich eine Kugelform hat. Anhand von einigen Animationen kann man lernen, wie man die Krümmung der Erde erkennen kann, bzw. unter welchen Umständen sie flach erscheint. Die Simulation kann auch Refraktion simulieren. Anhand von Fotos zeige ich, dass die Simulation die Realität abbildet, indem die berechneten Grafiken der Simulation den Fotos überlagert wird.
Curvature App: Simulation von Globus-Erde und Flat-Earth
Die Curvature App zeigt anhand des blauen Gitters, wie die Erdkrümmung in einer bestimmten Höhe unter einem bestimmten Bildwinkel erscheint. Der Bildwinkel kann auch als 35mm-Brennweite eingestellt werden (Brennweite umgerechnet auf die Standard-Bilddiagonale von 35 mm).
- Curve
- Causeway
- Soundly
- TrnsmLine
- Tensas
- Grace
- Chicago
- Canigou
- Bedford
- Custom
- Reset
Klicke oben um eine Demo zu starten. Klicke erneut um einen Schritt zu überspringen. Clicke die Animation für start/stop.
- Views
- Objects 1
- Objects 2
- Refraction
- Units
- Save/Restore
- <<
- Play
- >>
- 0
Bitte lies den Abschnitt Refraktion um dich mit diesem Panel vertraut zu machen.
Verwende dieses Panel um zwischen verschiedenen Längen-Einheiten umzurechnen. Du kannst per Copy/Paste die Resultate in die Felder der anderen Panels übernehmen.
Get App State Get App Url Set App State Compact Clear
Verwende dieses Feld um einen bestimmten Zustand der App mit Get App State zu erhalten und verwende Copy/Paste um den Zustand in einer externen Datei abzuspeichern. Verwende Copy/Paste um den gespeicherten Zustand von der Datei ins Fels zu kopieren und clicke dann auf Set App State um den Zustand zu aktivieren. Du kannst die Parameter in diesem Feld editieren und mit der Enter-Taste übernehmen.
Verwende Get App Url um eine URL für den aktuellen Zustand der App zu generieren. Clicke Set App State oder kopiere deie URL ins Adressfeld eines Browsers um zu dieser Seite zurückzukehren und den entsprechenden Zustand wiederherzustellen.
Perspective on a Globe
Wenn du Mühe hast zu verstehen, wie Perspektive auf einem Globus funktioniert
Comparison of Globe and Flat-Earth Model Predictions with Reality
für einen Seite-an-Seite Vergleich der Modell-Vorhersagen mit zugehörigen echten Bildern
Anhebungs Data-Werte
Wenn du die Option Show Data aktivierst, werden 3 Anhebungs-Werte in der Grafik angezeigt: Objekt Anhebung realitv zum Horizont, Objekt Angebung absolut und Horizont Anhebung. Diese Werte beschreiben die Änderungen in einer Szene, wie sie durch Refraktion hervorgerufen werden. Dies sind Werte wie sie in der Entfernung des nächstliegenden Objektes erscheinen. Wenn zum Beispiel die Horizont Anhebung mit 10 m angegeben wird, bedeutet das, dass der Horizont wegen Refraktion um 10 m angehoben erscheint, gemessen mit einer Messlatte an der Position des nächsten Objektes.
Die Anhebungs-Werte werden über Winkel zwischen Sichtstrahlen zu verschiedenen Punkten gemessen: Sichtstrahlen zur Basis des nächsten Objektes und zur Horizont-Linie für die Fälle mit und ohne Refraktion. Diese Winkelwerte werden dann in Höhenwerte umgerechnet, wie sie auf einer Messlatte oder einem M-Rod Objekt an der Position des nächsten Objektes abgelesen werden können.
Wenn du von oben auf ein M-Rod Objekt schaust, sodass es vertikal komprimiert erscheint, werden die Anhebungs-Werte entsprechend korrigiert, sodass sie immer noch auf dem jetzt verzerrten M-Rod abgelesen werden können. Wenn also zum Beispiel ein Anhebungs-Wert von 5 m angezeigt wird und eine 10 m Messlatte auf die halbe Höhe verzerrt erscheint, kann diese immer noch zum Ablesen der 5 m verwendet werden, obwohl auf einer senkrecht zur Sichtlinie stehenden Messlatte nur 2,5 m gemessen würden.
Ein Anhebungs-Wert entspricht immer dem Wert, wie er von der (komprimierten) Skala eines M-Rod Objektes an der Position des nächsten Objektes abgelesen werden kann.
Simulationsparameter
Die Simulationsparamter sind in die Panels Views, Objects 1, Objects 2 und Refraction gruppiert.
 Verwenung von URL Parametern zur Kontrolle der App
Verwenung von URL Parametern zur Kontrolle der App
Views Panel
Die Curvature App kann zum Vergleichen der kugelförmigen Erde (Globe-Earth) mit einer flachen Erde (Flat-Earth) verwendet werden. Die Darstellung des gewünschten Modells kann durch entsprechende Wahl bei Model ausgewählt werden:
- Globe zeigt Szenen wie sie auf einem Globus aussehen
- FE zeigt Szenen wie sie auf einer Flachen Erde aussehen würden
- G+FE X zeigt Globus und Flach-Erde nebeneinander, wobei die FE Darstellung gespiegelt wird
- G+FE || zeigt Globus und Flach-Erde nebeneinander, wobei das eine Modell direkt in das andere übergeht
Zum Vergleich mit einem Flat-Earth-Modell kann unter Grid mit der Einstellung Projected ein rotes Gitter eingeblendet werden. Das rote Gitter zeigt die Projektion des blauen Gitters auf die Ebene der flachen Erde. Für niedrige Höhen sind die Abweichungen zwischen blauem Kugelgitter und rotem flachem Gitter minim. So klein, dass durch Ausschalten des roten Gitters die Krümmung kaum erkannt werden kann.
Beachte, dass das Globus-Gitter keinen konstanten Gitter-Abstand hat, sondern es wird eine bestimmte Anzahl Gitterlinien innerhalb des Horizontes angezeigt, einstellbar bei Lines. Dies entspricht dem natürlichen Sehen, denn wir haben auf der Erde ja auch kein festes Gitter, das die relativen Abstände zeigt. Das bedeutet, dass der Gitterabstand mit der Entfernung des Horizontes variiert. Der effektive Abstand der Linien kann unter Berechnete Werte bei GridSpacing abgelesen werden.
Mit CameraAim kann man auswählen, auf welchen Punkt die Kamera zielt (Globe Horizon oder Flat-Earth Äquator FE-Eq) oder welche Bezugslinie (Betwn: Linie zwischen Globe-Horizont und FE-Äquator oder Eye-Lvl: Augenhöhe) in der Bildmitte gehalten werden soll, wenn Tilt = 0 ist.
View∠ (view angle θ = Bildwinkel oder Field of View FoV) und f (35 mm-äquivalente Brennweite = Zoom) sind gekoppelt über die Formel:
| (1) |
Bei View∠ können Werte im Bereich von 0,1° bis 160°, oder bei f Werte im Bereich von 3,81 mm bis 24 800 mm in die Wertefelder eingegeben werden. Die Regler decken einen kleineren Bereich ab.
Eye-Level zeigt eine Linie im unendlichen, welche den Abstand Height von der Oberfläche beim Punkt des Beobachters hat. Diese Linie ist also auf Augenhöhe des Beobachters und wird daher Eye-Level genannt (englisch für Augenhöhe).
Tangent zeigt die Tangente an den Globus-Horizont an. Diese ist praktisch, um kleine Krümmungen zu erkennen.
Data blendet diverse berechnete Werte direkt in die Grafik ein.
Objects Panels
Es gibt zwei identisch aussehende Object Panels. Man kann somit zwei unterschiedliche Sets von Objekten in einer Simulations-Szene kombinieren. Einige Objekte vom selben Typ können in den beiden Panels unterschiedlich aussehen, z.B. die T-Tower. Verwende das Panel Objects 1 für Objekt im Vordergrund und Objects 2 für Hintergrundobjekte. Die Objekte können in der Entfernung nicht gemischt werden, da der Zeichen-Algorithmus alle Objekt einer Gruppe zusammenfasst. Die Darstellung von gemischten Objekten ist optisch nicht korrekt.
Um Objekte in die Grafik einzublenden, muss bei NObjects ein Wert grösser als 0 eingestellt werden. Die Art des Objektes wird im unteren Bereich mit ObjType ausgewählt. Wenn dann kein Objekt sichtbar ist, ist es wahrscheinlich ausserhalb des Sichtbereiches. Verändere den Sichtbereich im Views Panel oder verschiebe die Objekte mit den anderen Parametern wie Dist in den Sichtbereich.
Die meisten Parameter in diesem Panel dürften selbsterklärend sein. Zu beachten ist, dass Zeilen, die mit derselben Farbe hinterlegt sind, miteinander in Beziehung stehen. So kann man mit den Radio-Buttons SideVar den Modus zur seitlichen Verschiebung der Objekte wählen und mit dem Regler SideVar kann die Grösser der Verschiebung eingestellt werden. Analoges gilt für SizeVar.
Refraction Panel
Hier werden alle Einstellungen der Refraktion vorgenommen. Für eine detailierte Beschreibung siehe Refraktion.
Units-Calculator Panel
Hier kann man Längenwerte in verschiedene Einheiten umrechnen. Sobald ein Wert in ein Feld eingegeben wird, werden alle andere Einheiten berechnet. Mann kann einen Wert aus einem dieser Felder per Copy/Paste in ein Feld in einem anderen Panel kopieren. Drücke die Esc Taste (gilt für alle Felder aller Panels) um das Feld zurückzusetzen.
Berechnete Werte Panel
Welche Daten diese Felder anzeigen, kann aus den darunter angezeigten Grafiken abgelesen werden. Die dort nicht angegebenen Daten sind:
AngDiameter (angular diameter = Sehwinkel) ist der Winkel, unter dem die Globus-Erde von einem Beobachter im Abstand Height gesehen wird.
GridSpacing ist der Gitterabstand des blauen Gitters der Globus Darstellung. Der Abstand kann im Panel Views mit der Option Lines vorgegeben werden.
DisplHorWidth gibt den horizontalen Abstand zwischen dem schwarzen Rahmen in der Entfernung des Horizontes an. Wenn der Horizont nicht gekrümmt und nicht geneigt ist, entspricht dies der Länge des Horizontes der innerhalb des schwarzen Rahmens liegt. Die Berechnung der Länge der effektiv sichtbaren gekrümmten Horizontlinie ist zu kompliziert als dass sie in eine Formel verpackt werden könnte. Aber dieser Wert kann als guter Schätzwert verwendet werden.
Refraktion
Die Curvature App kann beim Globus-Modell simulieren, wie sich die Refraktion auswirkt. Dazu kann im Panel Refraction die gewünschte Refraktion zum Beispiel mit dem roten Schieberegler eingestellt werden. Wenn die simulierte Grafik die Refraktion berücksichtigt, wird der entsprechende Wert unten in der Grafik eingeblendet. Ist die Refraction = 0, entfällt diese Anzeige.
Die Refraktion der Simulation kann entweder A) durch einen der Parameter Coeff. k, Factor a, Radius R' oder den roten Schieberegler direkt eingestellt werden. Oder die Refraktion kann B) aus den atmosphärischen Parametern Druck Press. P, Temperatur Temp. T und Temperatur-Gradient dT/dh berechnet werden. Im Fall B) wird die Refraktion berechnet, sobald der Wert in dT/dh geändert wird.
Die Parameter P, T und dT/dh können auch vom Std-Atmosphere Barometer im unteren Teil des Panels übernommen werden, indem BaroLink ungleich off gewählt wird. Das Barometer berechnet die Parameter für die Standard-Atmosphäre aufgrund der eingestellten Höhe Height h des Beobachters.
Achtung: Die Refraktions-Simulation macht nur Sinn unterhalb ca. 40 km Höhe. Wenn die Refraktion mit der Standard-Atmosphäre gekoppelt ist (BaroLink = Std-Atm) nimmt die Refraktion automatisch mit der Höhe enstprechend ab. Man kann jedoch beliebige Werte in die Felder eingeben, aber erhält dann unter Umständen unrealistische Refraktionen und/oder Temperatur-Gradienten dT/dh.
Was ist Refraktion?
Die Dichte der Atmosphäre nimmt generell mit der Höhe exponentiell ab. Jede Dichteänderung verursacht eine Lichtbrechung. Ist die Dichteänderung nicht abrupt sondern kontinuierlich wie in der Atmosphäre, wird das Licht nicht gebrochen, sondern gebeugt, genannt Refraktion. Licht wird immer in die Richtung der grösseren Dichte gebeugt, in der Atmosphäre also in der Regel nach unten. Das bedeutet, dass Objekte in der Ferne höher erscheinen, als bei gerader Sichtlinie. Dieser Effekt nimmt mit dem Abstand des betrachteten Objektes zu, da der Lichtstrahl eine grössere Strecke zurücklegt und sich daher die Krümmung mehr auswirkt.
Refraktion ist nicht ein konstantes Phänomen. Sie hängt stark von den aktuellen atmosphärischen Bedingungen entlang des Lichtpfades ab und schwankt daher auf dem Weg zum Beobachter. Da man die aktuelle Refraktion vom Objekt zum Beobachter unmöglich messen kann, nimmt man einen Durchschnittswert an, der aus den atmosphärischen Bedingungen am Ort des Beobachters berechnet werden kann, zumindest für kürzere Distanzen. Aber diese Werte können auch für längere Distanzen verwendet werden, wenn ähnliche Bedingungen entlang der Sichtlinie gelten. Der Durchschnittswert entspricht einem Lichtstrahl, der einem Bogen mit dem konstanten Radius RR folgt.
Weitere hilfreiche Informationen und Simulationen von Refraktionen:
- Atmospheric Refraction Phenomena
- Introduction to Superior-Mirage Simulations
- Curvature and Refraction in Surveying and Leveling Through History; Metabunk
- Standard Atmospheric Refraction: Empirical Evidence and Derivation; Metabunk
Refraktions-Parameter
Die Refraktion kann durch verschiedene Parameter ausgedrückt werden:
- Refraktions-Koeffizient k → Coeff. k
- Refraktions-Faktor a → Factor a
- Refraktions-Radius R' → Radius R'
- Refraktions-Winkel ρ → ObjRefr∠
Die Werte 1 bis 3 sind direkt miteinander verknüpft. Sobald einer dieser Werte vorgegeben wird, werden die anderen beiden daraus berechnet.
Refraktions-Koeffizient k
Der Refraktions-Koeffizient k ist das Verhältnis des Erdradius R zum Radius der Sichtlinie RR:
| (2) |
| |||||||||
| wobei' |
|
Wenn die Sichtlinie nicht gekrümmt ist, ist ihr Radius unendlich. Das bedeutet, dass bei einer nicht gekrümmten Sichtlinie der Refraktions-Koeffizient k = 0 ist. Wenn die Sichtlinie der Erdkrümmung folgt, was durchaus möglich ist, ist k = 1. Die Erde erscheint in diesem Fall völlig flach.
In der Vermessung wird oft ein Standardwert von k = 0,13 verwendet. Ein anderer häufig verwendeter Wert nimmt einen Krümmungsradius von RR = 7 · R an, was einem Koeffizienten von k = 0,142 enstpricht oder einem Refraktions-Faktor a von 7/6. Der Unterschied ist klein: auf 1000 m Entfernung macht das gerade mal 1 mm bei einer Höhenbestimmung aus.
Der Refraktions-Koeffizient kann aus den atmosphärischen Bedingungen wiefolgt berechnet werden (Quelle: Atmospheric refraction):
| (3) |
| ||||||||||||
| wobei' |
|
Für Standard-Atmosphäre ergibt dies einen maximalen Wert von ca. k = 0,17 der mit der Höhe des Beobachters kontinuierlich abnimmt und ab 40 km praktisch Null ist.
Der Temperatur-Gradient, d.h. die Temperaturänderung mit zunehmender Höhe, kann nahe der Oberfläche stark unterschiedlich sein. Während unter Standard-Atmosphäre bis in eine Höhe von 11 km eine Abnahme der Temperatur von 0,65°C pro 100 m angesetzt wird, d.h. dT/dh = −0,0065°C/m, können einige Meter oberhalb der Oberfläche stark unterschiedliche Werte gemessen werden. Entsprechend ist dann die Refraktion stark unterschiedlich.
Über kühlem Wasser oder Eis ist der Temperatur-Gradient dT/dh in einem Layer über der Oberfläche oft positiv, d.h. die Temperatur im untersten Layer der Atmosphäre nimmt mit der Höhe zu. Man spricht dann von einer Inversion. Ist der Temperatur-Gradient grösser als −0,01°C/m, also insbesondere bei einer Inversion, ist die Luft stabil (stabile Inversion). Ist der Temperatur-Gradient kleiner als −0,01°C/m, was bei kühler Luft über warmem Boden der Fall ist, enststehen Ausgleichsströmungen und die Luft ist unruhig, instabil.
Bei einer Inversion ist die Lichtbeugung nach unten am extremsten und kann so stark sein, dass der Lichtstrahl der Erdkrümmung folgt: k ≥ 1. In diesem Fall erscheint die Erde flach.
Ist der Temperatur-Gradient negativer als Standard, also dT/dh < −0,0065°C/m, was über einer warmen Oberfläche bei kühler Luft der Fall ist, wird der Lichtstrahl weniger gebeugt, die Refraktion k ist dann kleiner als Standard. Bei sehr starkem negativem Gradienten, wenn der Boden heiss ist, kann der Lichtstrahl sogar nach oben gekrümmt sein, d.h. der Refraktions-Koeffizient k ist dann negativ. Dies ergibt eine Fatamorgana oder Schichten oberhalb der Oberfläche erscheinen gespiegelt.
Beachte, dass selbst dann, wenn sich der Beobachter in grösserer Höhe befindet, wo der Bodeneffekt beim Beobachter entfällt, die Sichtlinie zu weit entfernten Objekten sich lange entlang einer kühlen Oberfläche wie dem Meer ausbreiten kann und daher entsprechend stark gekrümmt wird. Beobachtungen über das Meer oder einen grossen See lassen daher oft Städte, Inseln oder Berge erscheinen, die nach Berechnungsformeln, welche die Refraktion nicht berücksichtigen, hinter der Erdkrümmung verborgen sein müssten, siehe Animationen Chicago und Canigou.
Klassifizierung der Refraktion
Um ein Gespür für die Stärke und Auswirkung der Refraktion zu bekommen, habe ich den Werten folgende Klassifizierung zugeordnet:
| Koeffizient k | 0 bis 0,12 | 0,12 bis 0,18 | 0,18 bis 0,38 | 0,38 bis 0,58 | 0,58 bis 0,78 | 0,78 bis 1 |
|---|---|---|---|---|---|---|
| Bezeichnung | schwach | standard | moderat | stark | sehr stark | extrem |
Entsprechend habe ich dem Temperatur-Gradienten folgende Klassifizierung zugeordnet:
| dT/dh | kleiner −0,01°C/m | −0,01 bis 0°C/m | grösser 0°C/m |
|---|---|---|---|
| Bezeichnung | instabiler Layer | stabiler Layer | stabiler Layer; Inversion |
| Bemerkung | warme Oberfläche, kältere Luft | kalte Oberfläche, wärmere Luft |
Wenn eine Refraktion ungleich Null eingestellt wird, werden der Wert k und dT/dh und ihre Klassifizierungen in der Grafik unten angezeigt. Wenn die Refraktion mit BaroLink = Std-Atm aus den Werten für die Standard-Atmosphäre errechnet wird, wird dies mit der Klassifizierung Standard Atmosphäre angezeigt.
Wenn die Oberflächentemperatur kälter als der darüber liegende Layer der Atmosphäre ist, ist die Luft sehr stabil. Stabile Layer unterdrücken Konvektion und turbulentes Vermischen der Luft und behalten so ihre Struktur bei. Bei der Standard-Atmosphäre ist der Temperatur-Gradient nur −0,0065°/m. Sie ist daher schwach stabil.
Quelle: Atmospheric Temperature Profiles
Je positiver der Temperatur-Gradient ist, d.h. je kälter die Oberfläche gegenüber dem untersten Layer der Atmosphäre ist, umso grösser ist die Refraktion. Dies erklärt, warum bei Laser-Experimenten über einem gefrorenen See keine Krümmung der Erde festgestellt werden kann, weil die starke Refraktion das Laser-Licht der Erdkrümmung entlang biegt.
Kopplung der Refraktion an die Standard-Atmonsphäre
Der Refraktions-Koeffizient k kann aus der empirisch gefundenen Formel (3) aus den aktuellen atmosphärischen Bedingungen beim Beobachter berechnet werden.
Im Panel Refraktion kann man im unteren Bereich Std-Atmosphere Barometer die von der Höhe h abhängigen Werte für Druck P, Temperatur T und Temperatur-Gradient dT/dh für die Standard-Atmosphäre ablesen. Diese Werte sind definiert bis in eine Höhe von ca. 85 km, ab dann werden sie als NaN angezeigt.
Wenn man diese Werte zur Berechnung der Refraktion verwenden will, kann man bei der Option BaroLink die Einstellung Std-Atm wählen. Dann sind die Barometer-Werte der Standard-Atmosphäre mit den Refraktions-Berechnungen verknüpft. Wenn man einen anderen Temperatur-Gradienten einstellt aber Druck und Tempertur der Standard-Atmosphäre verwenden will, kann man die Option T,P verwenden. Mit off wird die Verknüpfung deaktiviert und man kann beliebige Werte für Temperatur und Druck einsetzen, auch solche, die keinen Sinn machen.
Bei den anderen Optionen von BaroLink sind Tempertur und Druck mit den Baro-Werten verknüpft, aber es kann eine feste Refraktion ausgewählt werden. Der zugehörige Temperatur-Gradient wird dann daraus berechnet. Die Refraktion kann aber auch mit dem Schieberegler beliebig eingestellt werden. Beachte, dass diese Einstellungen nur im unteren Bereich der Atmosphäre bis ca. 20 km sinnvoll sind, da die Refraktion in der Natur mit der Höhe abnimmt, und nicht konstant bleibt.
Refraktions-Faktor a
Damit die Formeln zur Berechnung der Verdeckung von Objekten durch die Erdkrümmung auch mit Berücksichtung der Refraktion verwenden zu können, gibt es einen Trick: Man ersetzt einfach in den Formeln den Erdradius R durch einen reduzierten Refraktions-Radius R', der aus dem Refraktions-Koeffizienten k berechnet werden kann. Den Umrechnungsfaktor bezeichne ich als Refraktions-Faktor a:
| (4) |
| ||||||
| wobei' |
|
Refraktions-Radius R'
Der Refraktions-Radius R', der in die Formeln für die Berechnung der Verdeckung eingesetzt werden kann, ist damit:
| (5) |
| |||||||||
| wobei' |
|
Wenn die Refraktion k ungleich Null ist, verwendet die Simulation des Globus R' anstelle des Erdradius R, um die optische Auswirkung der Refraktion zu simulieren.
Beachte, dass der Refraktions-Radius R' nicht dem Krümmungs-Radius RR des Lichtstrahls entspricht. Der Zusammenhang zwischen den Radien ist:
| (6) |
| |||||||||
| wobei' |
|
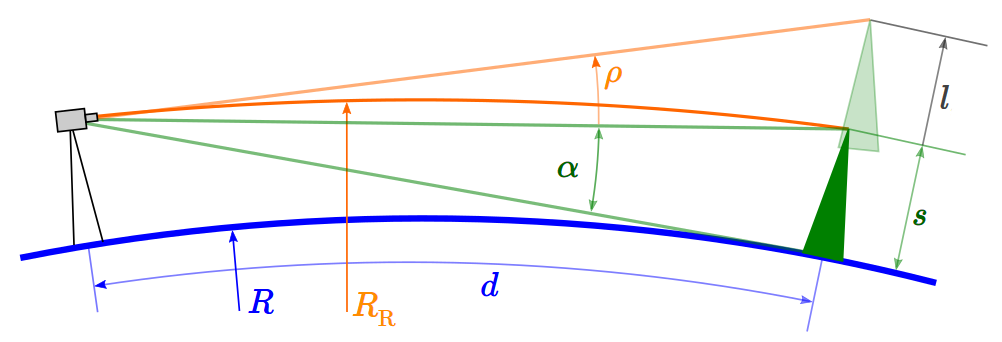
Refraktions-Winkel ρ
Analog wie die Grösse eines Objektes als Winkel-Grösse α (angular Size) angegeben werden kann, kann die Höhe, um welche ein Objekt angehoben erscheint, als Refraktions-Winkel ρ angegeben werden. Die Stärke der Anhebung hängt von der Refraktion k und der Entfernung des Objektes vom Beobachter ab. Je weiter entfernt ein Objekt ist, umso mehr erscheint es angehoben, weil der Lichtstrahl länger ist und somit über eine längere Strecke gekrümmt wird.
Die Winkel-Grösse α eines Objektes in Grad ergibt sich aus seiner Grösse s und seiner Distanz zum Beobachter d. Eine gute Näherung für grössere Distanzen, wenn d praktisch der Sichtd-Dstanz vom Beobachter zum Objekt entspricht, ist:
| (7) |
|
Die Berechnung des Refraktions-Winkels ρ ist aufwändig und wird mittels Vektorgeometrie von der Simulation berechnet. Im Wesentlichen wird die Position des höchten Punktes des am nächsten liegenden Objektes auf einer Kugel mit Radius R und auf einer Kugel mit Radius R' berechnet. Dann wird je ein Vektor vom Beobachter zu diesen beiden Punkten errechnet. Der Refraktions-Winkel ρ ist dann der Winkel zwischen diesen beiden Vektoren.
Wenn man die Grösse s des Objektes und seine Winkel-Grösse α kennt, kann man mit dem Refraktions-Winkel ρ die absolute Anhebung des Objektes l in Bezug auf Eye-Level berechnen.
| (8) |
|
Da die Winkel-Grösse α eines Objektes mit grösserem Abstand d abnimmt, sein Refraktions-Winkel ρ jedoch mit dem Abstand zunimmt, nimmt die absolute Anhebung l eines Objektes mit dem Abstand zum Beobachter erheblich zu. Befindet sich das Objekt weit hinter dem Horizont, nimmt auch seine Anhebung lrel bezüglich dem Horizont entsprechend zu, wenn auch nicht so stark, da sich der näher gelegene Horizont gegenüber Eye-Level ebenfalls anhebt, aber um einen entsprechend dem Abstand kleineren Betrag.
Ist zum Beispiel ein Berg 2000 m hoch und erscheint unter einer Winkel-Grösse von 0,5° und der Refraktions-Winkel ist 0,25°, so erscheint der Berg um 1000 m angehoben. Beachte, dass diese Berechnung ohne Wissen der Entfernung zum Objekt durchgeführt werden kann. Die Entfernung zum Objekt ist im Refraktions-Winkel enthalten. Ist der Berg nur 1000 m hoch, ist seine Winkel-Grösse auch nur halb so gross: 0,25°. Man erhält damit wieder dieselbe Anhebung von 1000 m wie für den grossen Berg, was beweist, dass die Anhebung nur von der Entfernung abhängig ist, nicht von der Objektgrösse.
Da sich der Horizont durch die Refraktion ebenfalls anhebt, erscheint die Anhebung eines Objektes, das hinter dem Horizont liegt, bezüglich dem Horizont entsprechend kleiner. Befindet sich das Objekt vor dem Horizont, senkt es sich bezüglich dem Horizont sogar ab, obwohl es absolut gesehen angehoben wird. Dies kommt daher, dass der weiter entfernte Horizont mehr als das Objekt angehoben erscheint. Je grösser der Abstand des Objektes vom Horizont ist, desto grösser wird die relative Anhebung/Absenkung bezüglich des Horizontes. Sehr weit entfernte Berge können daher um einen beträchtlichen Anteil ihrer Grösse hinter dem Horizont angehoben erscheinen. So kann die Refraktion hinter der Erdkrümmung verborgene Berge zu einem grossen Teil wieder sichtar machen.
Der Refraktions-Winkel, die Winkel-Grösse des Objektes und die relative und absolute Anhebung werden in der Simulation angezeigt, wenn die Option Show: Data im Panel Views aktiviert ist oder kann im Panel Refraction abgelesen werden.
Beobachtungen
Die Erde ist im Vergleich zu uns Menschen riesig: 12 742 000 m im Vergleich mit 2 m. So gross tatsächlich, dass wir nicht in der Lage sind, von der rOberfläche aus mit blossem Auge ihre Kugelform zu erkennen. Nur mit präzisen technischen Hilfsmittel können wir die Entfernung zum Horizont und dessen Absenkung aufgrund der Kugelform messen. Erst ab grosser Höhe oder aus dem Weltraum können wir die Kugelform von Auge klar erkennen.
Selbst in Höhen von mehreren Kilometern, wie zum Beispiel der Flughöhe von Ferkehrsflugzeugen, kann die Kugelform nicht immer eindeutig erkannt werden. Erst auf Weitwinkelaufnahmen kann eine leichte Krümmung festgestellt werden. Dabei muss man aber berücksichtigen, dass Weitwinkel-Objektive die Szene verzerren können. Auf billigen Kameras oder Smartphones kann die Krümmung daher nur eingeschränkt beobachtet werden.
Die Sichtbarkeit der Krümmung ist also von Höhe und Sehwinkel bzw. Brennweite abhängig!
Dass sich der Horizont gegenüber Eye-Level senkt, kann von blossem Auge nicht erkannt werden, da ja in der Natur keine Eye-Level Linie über dem Horizont schwebt. Auf entsprechenden Instrumenten wie einem Overhead-Display eines Flugzeugs kann diese Absenkung jedoch gemessen werden.
Überlagern des Gitters mit Fotos
Um zu zeigen, dass das berechnete blaue Gitter die Realität tatsächlich korrekt widerspiegelt, kann man das Gitter mit einem echten Foto zur Deckung bringen.
Damit ein Gitter in ein echtes Foto eingeblendet werden kann, sind folgende Angaben notwendig:
- Höhe, in welcher die Aufnahme der Erde gemacht wurde
- 35mm-Brennweite oder Bildwinkel der Aufnahme
- Seitenverhältnis des Bildes
- Die Linse darf keine Verzerrungen aufweisen, Fisch-Eye Linsen sind ausgeschlossen oder eine Linsenkorrektur muss angewandt werden, welche das Bild entzerrt.
Als Fotos eignen sich besonders Aufnahmen, die in grossen Höhen gemacht wurden, also zum Beispiel aus einem Flugzeug oder aus dem Weltraum. Bei niedrigeren Höhen ist die Krümmung kaum sichtbar.
Vorgehen:
Stelle die Höhe mit dem blauen Schieberegler ein oder gib den Wert im Eingabefeld des Schiebereglers ein. Wähle die Brennweite oder den enstprechenden Bildwinkel mit einem der schwarzen Regler. Wähle bei AspectRatio das Seitenverhältnis des Bildes. Mit den grünen Reglern Tilt und Roll kann der Blickpunkt und die Querlage dem Foto angepasst werden.
Schneide den Bereich im schwarzen Rahmen mit einem Programm wie dem Sniping Tool von Windows aus. Öffne das Foto in einem beliebigen Bildbearbeitungsprogramm. Füge den ausgeschnittenen Bereich des Gitters in einer neuen Ebene (Layer) überhalb des Fotos ein. Skaliere die Gitterebene so, dass das Seitenverhältnis beibehalten wird und die Gitterebene gleich gross wie das Foto wird. Stelle den Blendmode der Ebene auf multiplizieren (oder so ähnlich). Eventuell muss die Gitterebene noch etwas verschoben und gedreht werden, wenn die Einstellungen von Tilt und Roll nicht exakt dem Foto entsprechen.
Wenn alles korrekt ausgeführt wurde, müsste nun das Gitter genau mit dem Bild der Erdoberfläche übereinstimmen. Die folgenden Aufnahmen zeigen, wie das Resultat aussehen kann:
Bilder von der ISS
Die Internationale Raumstation ISS umkreist die Erde in einer Höhe von 400 km. Aus dieser Höhe zeigt sich die Erde in der Curvature App eindeutig als Kugel. Ich wollte nun überprüfen, ob die berechneten Grafiken der Simulation mit Fotos von der ISS übereinstimmen. Dazu habe ich Originalfotos gesucht, bei denen Daten zu verwendeter Kamera und Objektiv im EXIF-Format gespeichert sind. Denn in der Simulation muss ich die Brennweite einer Kamera eingeben, um die korrekte perspektivische Darstellung zu erhalten.
Ich habe solche Bilder auf der NASA Website gefunden. Nachfolgend sind zwei solche mit und ohne überlagertes Gitter der Simulation aufgeführt:

 Test, ob die Grafik der Simulation mit einem realen Bild von der ISS übereinstimmt:
Test, ob die Grafik der Simulation mit einem realen Bild von der ISS übereinstimmt:Height = 400 km; 35mm-Brennweite f = 28 mm; Format 3:2; Linienabstand 48,91 km
Aufnahmedatum: 16.09.2016 20:55; Quelle: NASA; Originalbild mit EXIF Informationen

 Test, ob die Grafik der Simulation mit einem realen Bild von der ISS übereinstimmt
Test, ob die Grafik der Simulation mit einem realen Bild von der ISS übereinstimmtHeight = 400 km; 35mm-Brennweite f = 28 mm; Format 3:2; Linienabstand 48,91 km
Aufnahmedatum: 16.09.2016 20:55; Quelle: NASA; Originalbild mit EXIF Informationen
- Bilder Tauschen
- Mit Gitter
- Ohne Gitter
Für das obige Bild habe ich eine Originalaufnahme der NASA verwendet. Das Bild wurde laut EXIF-Daten mit Photoshop bearbeitet, vermutlich nur in ein JPG konvertiert. Ich finde keine Spuren einer Bildmontage oder Manipulation und das Bildrauschen entspricht dem einer entsprechenden Kamera mit den gewählten Einstellungen.
Ich habe in der Simulation oben als Height = 400 km und als 35mm-Brennweite f = 28 mm eingestellt. Mit Tilt und Roll habe ich die Grafik entsprechend dem Foto gedreht und verschoben, weil der Fotograph nicht den Horizont anvisiert hat. Dann hab ich eine Bildschirmkopie der Grafik erstellt und diese zusammen mit dem Foto in Photoshop geöffnet. Die Grafik habe ich über das Foto auf eine neue Ebene gelegt und die Farben invertiert. Die Grafik und das Foto haben dasselbe Seitenverhältnis von 3:2. Die Grafik musste ich jedoch skalieren, damit sie dieselbe Grösse wie das Foto bekam. Danach habe ich mit der Überblendung negativ Multiplizieren die Grafik dem Foto überlagert.
Und siehe da, die Grafik passt genau auf das Foto. Die Linien haben laut Simulation einen Abstand von GridSpacing = 48,91 km. Der Gulf of Suez passt genau zwischen zwei Linien. In Google Earth nachgemessen bekomme ich ca. 50 km. Also auch dies passt zusammen.
Nachfolgend ein weiteres Bild der Erde aus der ISS fotografiert mit derselben Kamera. Das überlagerte Gitter der Simulation passt auch hier perfekt. Die graue Linie oben entspricht dem Eye-Level, d.h. dem Horizont einer flachen Erde.

 Ein weiteres Bild der Erde aus der ISS fotografiert.
Ein weiteres Bild der Erde aus der ISS fotografiert.Height = 400 km; 35mm-Brennweite f = 28 mm; Format 3:2; Linienabstand 48,91 km
Original image with EXIF Informations

 Ein weiteres Bild der Erde aus der ISS fotografiert.
Ein weiteres Bild der Erde aus der ISS fotografiert.Height = 400 km; 35mm-Brennweite f = 28 mm; Format 3:2; Linienabstand 48,91 km
Original image with EXIF Informations
- Bilder Tauschen
- Mit Gitter
- Ohne Gitter
Bilder eines Raketenflugs
Nachfolgend ein paar Bilder des Videos GoPro Awards: On a Rocket Launch to Space, welches mit einer GoPro4 Kamera mit Fischaug-Objektiv aufgenommen wurde. Ich habe die Linsenkorrektur von Adobe Lightroom darauf angewandt und die Bilder passen dann perfekt zu den von der Curvature App berechneten Gittern:
Height = 120 km, Brennweite f = 18 mm, Kamera GoPro4
Der Horizont hat nach der Anwendung der Linsenkorrektur auf allen Bildern an jeder Position exakt dieselbe Krümmung. Das heisst, die Linsenkorrektur hat die Bilder korrekt entzerrt.
Der Horizont ist nicht auf Augenhöhe
Flat-Earther behaupten, der Horizont liege immer auf Augenhöhe (Eye-Level), was für eine flache Erde sprechen würde. Die Definition von Eye-Level ist, dass eine Linie vom Auge des Beobachters zu einem fernen Punkt auf Augenhöhe genau einen 90° Winkel zur Lotrechten beim Beobachter bildet. Der weit entfernte Horizont einer flachen Erde würde scheinbar bis auf Eye-Level reichen und somit einen 90° Winkel bilden.
Den Neigungswinkel (dip angle) von Eye-Level zum realen Horizont kann man mit blossem Auge aber nicht abschätzen, da ein notwendiger Bezugspunkt am Horizont fehlt. Einfach geradeaus auf den Horizont schauen und behaupten, dieser sei immer auf Eye-Level, ist eine Behauptung die nicht stimmt. Dies gilt höchstens annähernd für niedrige Höhen. In einem Flugzeug auf 11 km Flughöhe senkt sich der Horizont um 3,36° nach unten (siehe DipAngle in der Curvature App). Das ist zwar eine deutliche Neigung, aber von Auge mangels Bezugslinie nicht zu erkennen.
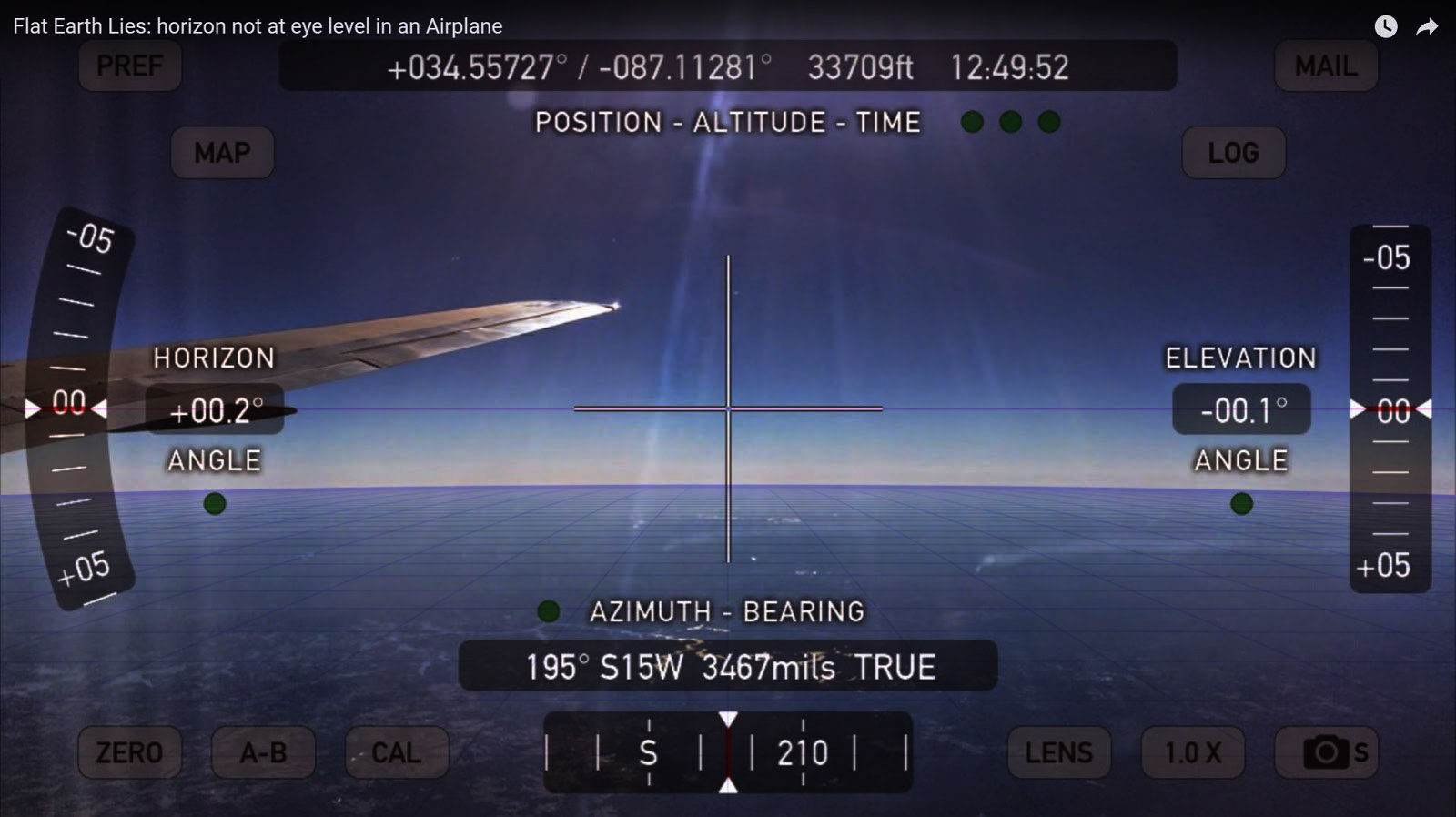
Das folgenede Foto wurde mit der Theodolite App mit einem iPhone aufgenommen. Das Flugzeug flog auf einer Höhe von ca. 33 709 ft (siehe Bild mitte/oben). Das iPhone wurde so ausgerichtet, dass das Fadenkreuz Eye-Level am Horizont anzeigt. Dies ist dann der Fall, wenn der ELEVATION ANGLE 0 anzeigt.
 Vergleich der effektiven Horizonthöhe mit Eye-Level-Höhe in einem Flugzeug.
Vergleich der effektiven Horizonthöhe mit Eye-Level-Höhe in einem Flugzeug.Height = 10,275 km; 35mm-Brennweite f = 33,9 mm; Format: 16:9; Linienabstand 8,035 km; Originalbild
 Vergleich der effektiven Horizonthöhe mit Eye-Level-Höhe in einem Flugzeug
Vergleich der effektiven Horizonthöhe mit Eye-Level-Höhe in einem FlugzeugHeight = 10,275 km; 35mm-Brennweite f = 33,9 mm; Format: 16:9; Linienabstand 8,035 km; Originalbild
- Bilder Tauschen
- Mit Gitter
- Ohne Gitter
Die Berechnung ergibt einen Dip-Winkel von 3,252°. Der Horizont liegt um 20,53 km unter Eye-Level und ist 361,6 km entfernt. Die eingeblendeten Gitterlinien haben einen Abstand von 8,035 km. Dies sind alles von der Simulation berechnete Werte.
Ich habe das Bild nicht selbst gemacht sondern bei BlogSpot gefunden. Es gibt eine Kopie davon auf meiner Website. Ich besitze die App Theodolite auf meinem iPhone und weiss wie sie funktioniert. Die Brennweite des iPhone habe ich aus dem Bildwinkel berechnet, den ich ebenfalls mit der App messen kann. Der berechnete Bildwinkel von 65° für die Diagonale stimmt mit Angaben im Internet überein. Er entspricht einer 35mm-Brennweite von 33,9 mm.
Die ermittelten Werte: Flughöhe 10,275 km, Bildwinkel 65° und Seitenverhältnis des Displays von 16:9 habe ich bei der Simulation eingegeben. Dann habe ich das Bild der Simulation am schwarzen Rahmen entlang ausgeschnitten, auf dieselbe Grösse wie das Foto skaliert und beides ineinander geblendet mit dem Blendmode multiplizieren. Wie man sieht, passt das berechnete Bild exakt auf das Foto und zeigt genau an, wo der Horizont der Erde bezüglich Eye-Level liegt. Beachte, dass eine ganz leichte Krümmung im Gitter erkennbar ist, aber auf dem Foto wegen dem Dunst am Horizont nicht mit Sicherheit ausgemacht werden kann.
Wie man mit einem einfachen selbst gebauten Tool den Horizont-Drop beobachten kann zeigt das folgende Video: Horizon Drop at Varying Altitudes. Flat Earth Debunked. von madmelon101.
Overhead Displays zeigen Eye-Level an

 Rockwell Collins’ Head-up Guidance System (HGS™) blendet kritische Fluginformationen in den Sichtbereich des Piloten ein und bietet Flugpfad-Unterstützung in allen Phasen des Fluges. Quelle: Rockwell Collins; Mit freundlicher Genehmigung
Rockwell Collins’ Head-up Guidance System (HGS™) blendet kritische Fluginformationen in den Sichtbereich des Piloten ein und bietet Flugpfad-Unterstützung in allen Phasen des Fluges. Quelle: Rockwell Collins; Mit freundlicher GenehmigungFlugzeuge können mit Overhead Displays ausgerüstet werden. Diese Displays werden zwischen Pilot und Frontfenster geschoben. Wenn der Pilot durch dieses Glasdisplay aus dem Fenster voraus schaut, kann er die wichtigsten Flugaten wie künstlicher Horizont, Geschwindigkeit, Flughöhe, vertikale Geschwindigkeit, Flugrichtung, ja sogar die Piste und neuerdings auch das Gelände wie bei einem Nachtsichtgerät sehen. Bemerkenswert ist, dass die angezeigte Grafik sich mit der Kopfbewegung des Piloten mitbewegt. Es sieht so aus, als würde die Grafik in das Gelände projiziert.
Fliegt nun das Flugzeug auf grosser Höhe, im Bild auf 39 000 ft, liegt der echte Horizont aufgrund der Erdkrümmung ca. 3,5° unterhalb des Eye-Levels. Das Display projiziert eine horizontale Linie auf Eye-Level in die Szene. Im Bild kann man deutlich den Abstand zwischen der Eye-Level-Linie und dem echtem Horizont sehen.
Das stilisierte Flugzeug im Display zeigt die effektive Flugrichtung an. Im Bild liegt das Symbol auf der Eye-Level-Linie, was bedeutet, dass das Flugzeug weder steigt noch sinkt. Es liegt hier deutlich links von der Mitte, was bedeutet, dass das Flugzeug wegen Seitenwind von vorne/rechts (siehe Pfeil links oben) nicht geradeaus fliegt, sondern mit dem Wind seitlich nach links geschoben wird. Das Flugzeug muss diese Abweichung korrigieren, indem die Nase dem Pfeil enstprechend in den Wind gerichtet wird, damit es das Ziel nicht verfehlt. Der Autopilot nimmt diese Korrektur automatisch vor.
 More evidence the Horizon does not remain at eye level as you gain altitude.; Erklärung eines Piloten.
More evidence the Horizon does not remain at eye level as you gain altitude.; Erklärung eines Piloten.
Kommentare
Wow
Das ist ein bemerkenswertes Stück Arbeit. Ich hab zu diesem Thema keine vergleichbar ausführliche und unprätensiösere Herangehensweise gesehen. Das ist toll.
Liebe Grüße
Flo
Sehr interessanter Bericht. Danke für deine sachliche Herangehensweise.
Aber diese GoPro Aufnahmen auf youtube sehen sehr nach Animation aus. Deshalb werden auch deine Berechnungen auf eine Kugel hinweisen, was nicht ausschließt, daß die Erde flach ist.
Meine bisherigen Forschungen deuten auf eine flache Erde hin. See vermessen mit Zoomfotos. Momentan beschäftige ich mich mit Bergen mit Bezug auf fallenden Horizont/Augenhöhe.
Derzeitige Quellen: http://schafberg.panomax.com, Ausgangspunkt: Schafberg, Ziel ist der Berg Großer Traithen, Entfernung 105 km
Im Sommer dann Lokalaugenschein mit Wasserwaage am Berg! ;)
GoPro Aufnahmen
Ich komme zu einem anderen Schluss bezüglich der GoPro Aufnahmen. Das Video ist echt und zeigt den ganzen Flug aus verschiedenen Perspektiven. Ich finde nicht den leisesten Hinweis einer Animation.
Meine Berechnungen wissen nichts vom Bild, mit dem sie überlagert werden. Sie simulieren einfach ein bestimmtes Kamerabild in einer bestimmten Höhe. Wenn die Daten eines Fotos bekannt sind (Höhe und Bildwinkel oder Brennweite, verwendete Linsen) muss die Berechnung mit dem Bild deckungsgleich sein - was hier offenbar der Fall ist. Du kannst ruhig davon ausgehen, dass die Bilder oben (nach der angewandten Linsenkorrektur) die echten Verhältnisse zeigen.
Die ISS-Fotos
Die ISS-Fotos wurden mit Digitalen Profi-Kameras mit guten verzerrungsarmen Linsen gemacht. Ich finde keinerlei Hinweise einer Manipulation oder Animation oder CGI Spuren, wenn ich das Bild noch so sehr in Photoshop analysiere.
Die ISS ist echt. Man kann sie Online virtuell begehen und sie wird in Videoclips von den Astronauten bis ins Detail erklärt. Diese Aufnahmen kann man nicht so perfekt fälschen. Manche Dinge kommen einem im ersten Moment vielleicht auffällig ungewöhnlich vor. Aber das kommt daher, dass wir keine Erfahrung mit Schwerelosigkeit haben. Für uns sieht alles auf der ISS ungewohnt aus. Das hat nichts mit fake zu tun. Unser Gehirn ist einfach anders konditioniert worden.
 360° Panoramafotos aus der Raumstation ISS
360° Panoramafotos aus der Raumstation ISS
Zoom-Fotos zum Nachweis der Krümmung/Flachheit
Dein Vorhaben mit den Zoom-Fotos ist so eine Sache. Mit solchen Verfahren kann man die Krümmung nicht zuverlässig messen, weil einem die Refraktion immer einen unberechenbaren Streich spielt. Das beweise die vielen widersprüchlichen Videos und Fotos im Netz.
Hier ein Auszug aus der Wikipedia, der dies erklärt:
Effect der atmosphärischen Refraktion
Unter Verwendung von Kilometer für d und R, und Meter für die Höhe h, und für den Radius der Erde R = 6371 km, wird die Distanz zum Horizont ungefähr (vereinfachte Formel):
- d ≈ 3,57 · √ h
Normalerweise ist die Dichte der Luft über der Oberfläche der Erde grösser als in der Höhe. Dies macht den aktuellen Abstand zum Horizont grösser als nach der Berechnung mit den geometrischen Formeln. Unter Standardatmosphäre ist der Unterschied etwa 8%. Dies ändert den Faktor von 3,57 zu 3,86.
Wenn die Bedingungen unüblich sind, was nahe der Oberfläche praktisch immer der Fall ist, stimmt die Berechnung nicht. Refraktion ist stark abhängig von Temperaturgradienten, die von Tag zu Tag beachtenswert variieren, vor allem über kaltem Wasser.
In Extremfällen, wenn warme Luft über kaltem Wasser liegt, kann die Refraktion das Licht hunderte Kilometer weit entlang der Wasseroberfläche führen! Das Resultat ist dann, dass die Erde scheinbar flach ist.
https://en.wikipedia.org/
Da ist kein Wunder, dass man oft keine eindeutige Krümmung sehen kann oder jeder Versuch eine andere Krümmung ergibt. Die Zoom-Versuche ergeben nur nutzlose Daten, da die Refraktion nicht gemessen werden kann. Daraus Schlüsse ziehen zu wollen ist Zeitverschwendung - kann man nicht. Als Studium der Refraktionseffekte jedoch allemal interessant.
Messen des Abfalls des Horizontes
Das ist schon leichter zu messen, vorausgesetzt man hat das richtige Werkzeug: einen Theodoliten, der den Dip-Winkel gegenüber Eye-Level bis auf Bruchteile von Graden messen kann. Denn in Bergeshöhe gibt es nur ein/zwei Grad Absenkung. Zudem ist dort der Horizont keine Ebene, ausser am Meer.
Ich empfehle Dir mindestens die oben erwähnte Theodolite App zu verwenden. Die kostet nur ein paar Franken und könnte für diese Zwecke ausreichen. Man kann die Versuche auch gleich abfotografieren.
Viel Spass beim Forschen.
Grossartige Seite, ich bin begeistert!
Grossartig, ihr tut wirklich alles um die Menschen zu verarschen :)
@Jupp, autsch!
Es ist überhaupt nicht mein Ziel, irgend jemanden zu verarschen. Ich habe diese Seite komplett alleine und unabhängig erstellt und programmiert. Mich hat einfach nur interessiert, ob die u.a. von NASA präsentierten Fotos und Fotos von Amateur-Raketenflügen mit dem allgemein akzeptierten Modell der Globus-Erde übereinstimmen oder nicht. Ich wollte herausfinden, weshalb man von Auge so schwer die Krümmung der Erde erkennen kann. Zudem wollte ich sehen, ob sich ein optischer Unterschied zwischen den beiden Modellen ergibt, wie er quantitativ aussieht und ob er einfach zu messen ist.
Ich denke, ich konnte zeigen, dass die publizierten Bilder der ISS, der Raketenflüge und Aufnahmen aus einem Flugzeug mit dem Globus-Modell perfekt übereinstimmen. Ich konnte zeigen, dass es messbare Unterschiede zwischen beiden Modellen gibt, insbesondere beim Absenken des Horizontes. Meine Simulation zeigt, dass dieser Unterschied ohne Messungen von Auge NICHT erkennbar ist, mangels Referenz auch nicht aus grossen Höhen. Ich zeige auf, mit welchen Instrumenten das Absenken gemessen werden kann und wie gross diese Werte sein müssten. Die Berechnungen stimmen exakt mit den Messungen von Head-up Systemen in Flugzeugen und mit der Theodolite-App überein.
Die Resultate sprechen eindeutig für das Globus-Modell und gegen das Modell einer flachen Erde. Die Resultate können mit vertretbarem Aufwand (Theodolite App und Reise in einem Flugzeug) selbst nachgeprüft werden.
Ich möchte betonen, dass die von mir erstellten Programme nicht dahingehend manipuliert sind, irgend ein Modell zu bevorzugen. Der Code der Simulation ist öffentlich einsehbar! Ich konnte mit unabhängig von mir gemachten Fotos zeigen, dass die Simulation offensichtlich die Realität gut nachbildet. Die Resultate sind reproduzierbar und können von jedem nachgeprüft werden.
Hallo,
Wenn man auf dem Boden steht, dürfte man 50 km weiter laut der erdkrümmung nicht den Boden sehen können! Anhand der Berechnungen. Wieso sieht man denn doch was? Siehe das aktuelle Video Bodensee. Oder Salzsee wo man 156km weit entfernt das Ufer sehen kann. Augenhöhe ist dann ca 1,7 m.
Da stimmt doch was nicht? Oder behaupten sie auch es sei eine Spiegelung oder Fatamorgana? Werte einfach mal in die Tabelle eintragen!
Hallo Frank
Hast Du meinen Kommentar unter Effect der atmosphärischen Refraktion gelesen? Die Sichtlinie zum Horizont ist ganz selten eine gerade Linie, sondern wird aufgrund der Temperatur- und Druckänderungen der Atmosphäre nahe dem Boden nach unten gekrümmt (Refraktion). Das bedeutet, dass man z.T. wesentlich weiter sehen kann, als die Berechnungen mit der Geraden ergibt.
In Extremfällen, z.B. wenn warme Luft über kaltem Wasser liegt, kann die Refraktion das Licht hunderte Kilometer weit entlang der Wasseroberfläche führen! Das Resultat ist dann, dass die Erde scheinbar flach ist.
Quelle Wikipedia: Effect of atmospheric refraction
Unter Landvermessern und Seefahrern ist diese Tatsache schon seit Jahrhunderten bekannt.
Verdeckung aufgrund der Erdkrümmung mit Refraktion
Im excellenten Video FLAT EARTH - EXPERIMENT - TELESCOPE vom 01.08.2016 zeigt der Autor Alex Chertnik, wie man Messungen mit dem Teleskop über Wasser richtig macht und dokumentiert. Er misst über die 3 Distanzen 47,35 km, 41,32 km und 41,22 km an verschiedenen Tagen und zu unterschiedlichen Tageszeiten, wieviel von 4 ca. 300 m hohen Kaminen durch die Krümmung der Erde verdeckt wird.
Im Gegensatz zu allen Flat-Earth Videos berücksichtigt er in seinen Berechnungen die Refraktion. Seine Messungen stimmen exakt mit den Berechnungen für eine Globus-Erde mit Radius 6371 km unter Berücksichtigung der Standard-Refraktion überein.
Im Video ist deutlich zu sehen, wie das Bild aufgrund der Schwankungen der Refraktion wackelt und flimmert und dass der Horzont nicht eine klare horizontale Linie ist sondern wellenförmig hin und her laufende Verzerrungen zeigt. Diese Wellen stammen nur zu einem kleinen Teil vom Wasser selbst, sondern entstehen durch die Refraktion. Die Verdeckung schwankt aufgrund dieser Refraktionswellen um etliche Meter.
Das Video beweist sehr deutlich, dass die Erde eine Kugel sein muss!
Hinweis: Wenn Du mit der Standardrefraktion von 7/6 · R in meiner Berechnung oben rechnen willst, kannst Du als Erdradius 7433,1 km eingeben. Aber wie gesagt, die Refraktion direkt über Wasser kann wesentlich höher sein!
Ein paar nützliche Links zur Refraktion aus dem Video:
- Refraction calculator app: https://www.metabunk.org/
curve/ - Refraction info: https://www.dropbox.com/
s/ uonad2glir1nb7x/ 01%20refraction.docx? dl=0
Moin Walter,
alles schön und gut, was Du hier argumentativ vertrittst. Die von Dir verwendete Herangehensweise an dieses Thema zeigt allerdings Deine - meiner Meinung nach - nicht ausreichend kritischen Denkmuster.
Ich möchte Dich mal auf eine Sache hinweisen:
Die bisher nicht wahrheitsgemäß beantwortete Frage, warum es keine echten, unbearbeiteten Fotos gibt, welche den "Planeten" Erde in ihrer Gesamtheit zeigen - weder von NASA, ESA, CNSA, ISRO oder der russischen Роскосмос (Roskosmos).
Denn die "Fotos", die es gibt, zeigen alle eine perfekte Kugelform - obwohl der wissenschaftliche Konsens ist, dass die Erde die Form einer an den Polen abgeflachten Kugel haben soll.
Und wo sind bei den Darstellungen der Erde, sowie den angeblichen Live-Übertragungen der NASA, die über 13.000 (aktiven und inaktiven) Satelliten zu sehen, die angeblich um die Erde kreisen? Eine accurate dreidimensionale Simulation der vorgeblichen Objekte in Umlaufbahn findest Du hier: http://apps.agi.com/
Wenn die Erde wirklich eine sich (am Äquator) mit mehr als 1666 km/h ostwärts um die eigene Achse drehende Kugel wäre, wie kann man dann die folgenden Phänomene erklären?
1) Warum haben wir keinen dominierenden Westwind, sondern ständig wechselnde Windrichtungen - sogar in Richtung der angeblichen Rotation? Durch die wissenschaftlichen "Fakten", dass die Erde (a) kein geschlossenes System ist und (b) Masseträgheit existiert, müsste die Trägheit der Atmosphäre dafür sorgen, dass eben dieser vorherrschende Westwind fast durchgehend auftritt.
2) Warum müssen Ingenieure, Statiker und Architekten die Erdkrümmung nicht in ihren Berechnungen für z.B. Brückenkonstruktionen berücksichtigen?
3) Weshalb korrigieren Flugzeuge ihre Flugbahn nicht in kurzen Intervallen, um der postulierten Erdkrümmung folgen zu können? Die Fliehkraft von beschleunigten Flugzeugen müsste definitiv stärker sein als die angeblich auf sie wirkende "Gravitation" in höherem Abstand von der Erde...
Ich habe noch viel mehr Fragen, falls Interesse Deinerseits an einer vollwertig- und bereichernden Diskussion besteht ;-)
Ich bin davon überzeugt, dass man die herrschende Religion namens Wissenschaft mithilfe ihres eigenen pseudowissenschaftlichen Systems zur Thesenvalidierung komplett auf den Kopf stellen könnte!
Zudem finde ich, dass man immer darauf achten sollte, wie Kritiker eines vorherrschenden Erklärungssystems (Religion &/ Wissenschaft) behandelt werden, wenn sie es auch nur wagen sollten, nicht nur eine verständliche und logisch schlüssige, sondern eine zudem emotional befriedigende Erklärung von grundlegenden Theorien zu verlangen...
PS: Nicht zu vergessen, die herrschende Elite hatte mehrere Jahrhunderte Zeit, ihre wissenschaftlichen Formeln und Erklärungen so zu formulieren (verklausulieren), dass sie zum propagierten Universum-Modell passen...
Mit freundlichen Grüßen,
Kay
Hallo Kay
Echte Fotos von der Erde
- Ich möchte Dich mal auf eine Sache hinweisen: Die bisher nicht wahrheitsgemäß beantwortete Frage, warum es keine echten, unbearbeiteten Fotos gibt, welche den "Planeten" Erde in ihrer Gesamtheit zeigen - weder von NASA, ESA, CNSA, ISRO oder der russischen Роскосмос (Roskosmos). Denn die "Fotos", die es gibt, zeigen alle eine perfekte Kugelform - obwohl der wissenschaftliche Konsens ist, dass die Erde die Form einer an den Polen abgeflachten Kugel haben soll.
Die Bilder sind schon echt. Und Bilder, welche die ganze Erde zeigen sind praktisch immer bearbeitet. Das hat mit ihrer Entstehung zu tun. Ich werde das gleich erklären.
Natürlich gibt es von anderen Planeten, Satelliten und anderen Weltraumdingen, wie von allem in der Welt, auch CGI Material, aber das wird in der Regel dann auch so bezeichnet. Manchmal werden Fotos auch "aufgepeppt", wie es halt in der Werbung üblich ist. Deswegen gleich die Kugel-Erde als Fake bezeichnen? Ist ein Fotomodell auch Fake, wenn ihr Foto aufgepeppt worden ist?
Die Echtheit der Bilder der Erde wird von Flat-Earthern angezweifelt, weil sie nicht dem entsprechen, was sie sich vorstellen. Ja wie müsste die Kugel-Erde denn ihrer Meinung nach aussehen? Muss die Erde auf jedem Bild genau gleich aussehen? Wieso sollte sie das? Mach ein paar duzend Aufnahmen von Deinem Kopf zu verschiedenen Tageszeiten, aus verschiedenen Winkeln und verschiedenen Abständen und verschiedenen Kameras. Sind alle Aufnahmen gleich? Sind die Farben identisch? Wenn die Erde aus kurzer Distanz aufgenommen wird, sieht man nur einen kreisförmigen Ausschnitt der ganzen Erde und die Kontinente erscheinen daher vergrössert und verzerrt. Mach mal ein Selfie aus sehr kurzer Distanz vor deiner Nase und diese wird auch überproportional gross auf dem Bild erscheinen. Fake? Nein - das ist jetzt eben Perspektive!
Warum sind viele der Aufnahmen der ganzen Erde bearbeitet? Praktisch alle digitalen Aufnahmen sind irgendwie bearbeitet. Auch deine Digitalkamera muss die Bilder vom Sensor bearbeiten: Die rohen Sensordaten bestehen nämlich aus den drei Grundfarben rot, grün und blau und müssen vom Kameraprozessor zuerst zu einem einzigen Bild zusammengerechnet werden. Die Daten werden zudem noch weiter vom Prozessor in diversen Schritten optimiert und schliesslich komprimiert. Das alles geschieht in einem Schritt, weil die Kamera alle Grundfarben mit einem einzigen Sensor aufnehmen kann, der einen Filter mit einem RGB-Pixelmuster davor hat. Siehe Digitalkamera auf Wikipedia.
Wetter-Satelliten arbeiten anders. Sie haben keine Kameras an Bord, die Echtfarbbilder mit einer einzigen Belichtung aufnehmen können. Es handelt sich bei den Kameras um spezialisierte Multispektralkameras. Diese enthalten einen CCD-Chip, der nur Helligkeitsunterschiede aufnimmt, keine Farben. Er ist dafür aber über einen wesentlich grösseren Spektralbereich empfindlich als komerzielle CCD-Sensoren. Vor dem CCD-Sensor gibt es ein Rad mit unterschiedlichen Spektral-Filtern. Will man zum Beispiel eine Infrarotaufnahme mit einer Wellenlänge von 900 nm machen, wird der entsprechende Filter vor den Sensor gedreht und eine Aufnahme gemacht. Auf dieser Aufnahme erscheint dann z.B. die Vegetation besonders klar, sogar durch die Wolken hindurch. So gibt es für jeden Zweck einen eigenen Filter. Die rohen Sensordaten mit den Helligkeitsinformationen werden unbearbeitet an die Erde gefunkt.
Will man nun Echtfarbaufnahmen der Erde machen, müssen drei Aufnahmen hintereinander gemacht werden. Je eine mit einem Filter für die drei Grundfarben. Das ergibt dann 3 verschiedene Bilder mit Helligkeitsinformationen zu jedem Farbkanal, die hintereinander an die Erde gefunkt werden. Erst dort werden sie dann zu einem einzigen Farbbild zusammengesetzt. Das nennt man dann Composit-Aufnahme. Der Unterschied zu einer normalen Digitalkamera ist eigentlich nur, dass beim Satelliten der Signalprozessor nicht in der Kamera steckt, sondern in einem PC auf der Erde, was viel flexibler ist, weil man damit mehr als nur Echtfarbbilder erstellen kann. Das bedeutet aber nicht, dass diese Bilder nicht echt sind! Da wurde nichts hinzugefügt oder entfernt. Sie zeigen die Erde so, wie sie ist.
Auf der Seite Echtfarb-Aufnahmen der Erde vom Satelliten Himawari der JMA siehst Du ein paar Beispiele solcher Aufnahmen und viele Links zu Seiten, wo Du solche Bilder fast in Echtzeit herunterladen kannst. Dort kannst Du aber auch die Infrarotaufnahmen usw. herunterladen. Diese Bilder werden von den meteorologischen Instituten verwendet um Wetterprognosen zu erstellen.
Klingt alles an den Haaren herbeigezogen? Nun, Technik ist nicht immer so einfach, wie es scheint. Das kann ich Dir als Ingenieur versichern. Nur weil etwas einfach sein muss oder aussieht, ist es das noch lange nicht!
Form der Erde
- Denn die "Fotos", die es gibt, zeigen alle eine perfekte Kugelform - obwohl der wissenschaftliche Konsens ist, dass die Erde die Form einer an den Polen abgeflachten Kugel haben soll.
Hat sie auch. Aber du musst genauer hinhören oder nachfragen, wie gross die Abweichung von der perfekten Kugel ist! Ich kann Dir sagen, wie gross diese Abweichung ist:
Die Erde hat am Äquator einen Durchmesser von 12 756,274 km und an den Polen einen Durchmesser von 12 713,504 km, ist also leicht oblate spheroid. Der Unterschied ist nur 42,8 km - im Vergleich zu mehr als 12 700 km Durchmesser. Diese Abweichung von der perfekten Kugelform sieht man nicht von Auge auf einer Aufnahme. Der Satellelit Himawari 8 hat eine Sensorauflösung von 11 000×11 000 Pixeln, das sind 121 MegaPixel. Die Erde füllt diesen Sensor praktisch voll aus. Wegen der Abflachung sollte die Erde ca. 40 Pixel weniger hoch als breit erscheinen.
In der Landesvermessung muss man diese ellipsoide Form berücksichtigen. GPS-Koordinaten beziehen sich übrigens auf dieses sog. Referenzellipsoid. Das Referenzellipsoid entspricht der Oberfläche, welche die Erde haben würde, wenn sie nur aus Wasser bestehen würde. Die Erdfigur und das Erdschwerefeld kann heute auf wenige Zentimeter bzw. auf 0,0001% berechnet werden. Man weiss, dass die Abplattung auf der Südhalbkugel minimal stärker ist als im Norden. Daher kommt das Schlagwort Birnenform (Quelle).
Warum sind die Satelliten nie sichtbar auf Aufnahmen?
- Und wo sind bei den Darstellungen der Erde, sowie den angeblichen Live-Übertragungen der NASA, die über 13 000 (aktiven und inaktiven) Satelliten zu sehen, die angeblich um die Erde kreisen?
Auch hier wieder das Problem der Relationen. Verglichen mit der Grösse der Erde und dem nahen Weltraum drum herum sind 13 000 Satelliten nichts. Nur zm Vergleich: Nehmen wir mal 13 000 Autos und verteilen sie auf die Städte der Erde mit mehr als 100 000 Einwohnern, wovon es ca. 30 000 bis 50 000 gibt. Das gibt nur ein Auto für alle 2-3 Städte. Und dazu kommt noch, dass der Weltraum nicht nur eine Ebene ist, sondern 3-dimensional, also unendlich viele Ebenen hat. Da muss es schon mit dem Teufel hergehen, wenn Satelliten in Sichtweite kommen oder gar zusammenstossen. Ist aber schon mal passiert, weil Satelliten nicht wahllos um die Erde kreisen, sondern spezielle Bahnen haben, die sich an den Polen vermehrt kreuzen, siehe Satellitenkollision am 10. Februar 2009.
Warum kann man nie Satelliten aus dem Weltraum sehen? Erstens sind sie zu klein und zweitens zu dunkel im Vergleich zur Erde, ausser sie spiegeln gerade die Sonne zum Objektiv der Beobachters.
Wie gross ein Objekt erscheint hängt von seiner effektiven Grösse und der Distanz zum Objekt ab. Man kann dies durch den Sichtwinkel ausdrücken, den das Objekt beim Beobachter einnimmt. Der Sichtwinkel α errechnet sich wiefolgt:
| (9) | ||||||||||
| wobei' |
|
Machen wir ein Beispiel: Ein Satellit habe eine Seitenlänge s = 10 m und sei in einer Distanz von nur d = 100 km. Dann nimmt der Satellit einen Sichtwinkel von 0,0057° ein. Eine Kamera hat bei der Zoom-Brennweite von 100 mm einen Bildwinkel von 24,4°. Nehmen wir eine Kamera mit einem 12 MP Sensor, also 4000×3000 Pixel. Damit ein Objekt auf der Aufnahme 1 Pixel gross erscheint, muss es mindestens einen Sichtwinkel von 24,4°/3000 = 0,0081° einnehmen. Der Satellit in diesem Beispiel würde also fast ein Pixel gross erscheinen. Mit einem 1000 mm Zoom würde der Satellit in dieser rel. kurzen Distanz ca. 7 Pixel gross erscheinen.
Nun sind aber Satelliten mindestens einige zehntausend Kilometer von einem geostationären Satelliten entfernt, der Aufnahmen der ganzen Erde machen kann. Mit jeder Verzehnfachung der Entfernung wird der Sichtwinkel um den Faktor 10 ab. Der Satellit in 10 000 km Entferung erscheint unter einem 100 mal kleineren Winkel. Man müsste also ein 10 000 mm Zoom haben, dass dieser Satellit auch nur 1 Pixel gross erscheinen würde.
Mit einem Trick kann man in der Sonne stehende Satelliten nachts aufnehmen, indem man lange belichtet. Die Photonen, die das entsprechende Pixel in dieser Zeit treffen, summieren sich zu einem deutlichen Signal. Der Satellit wäre zwar viel kleiner als ein Pixel, aber die Kamera kann keine kleineren Objekte ablichten, daher gibt es einen Bildpunkt, der mindestens ein Pixel gross ist. Wenn man überbelichtet, kann die Ladung des Pixels in benachbarte Pixel überfliessen, sodass sogar ein weisser Fleck von mehreren Pixeln grösse entsteht. Was aber nicht heisst, dass der Satellit entsprechend gross ist.
Dieses Überfliessen von Ladung im CCD ist übrigens der Grund dafür, weshalb die Sonne hoch am Himmel viel grösser erscheint, als sie effektiv wäre. Steht die Sonne tief, ist das Licht abgeschwächt und das Überfliessen ebenfalls. Die Sonne erscheint dann kleiner als am Mittag. Deshalb muss man so starke Lichtfilter verwenden, dass keine überschüssige Ladung überfliessen kann, wenn man die wirkliche Grösse der Sonne aufnehmen will.
Atmosphäre und Erdrotation
Auf die folgenden Fragen kann ich im Rahmen dieses Kommentares nur kurz eingehen.
- Wenn die Erde wirklich eine sich (am Äquator) mit mehr als 1666 km/h ostwärts um die eigene Achse drehende Kugel wäre, wie kann man dann die folgenden Phänomene erklären?
- 1) Warum haben wir keinen dominierenden Westwind, sondern ständig wechselnde Windrichtungen - sogar in Richtung der angeblichen Rotation? Durch die wissenschaftlichen "Fakten", dass die Erde (a) kein geschlossenes System ist und (b) Masseträgheit existiert, müsste die Trägheit der Atmosphäre dafür sorgen, dass eben dieser vorherrschende Westwind fast durchgehend auftritt.
1. Die Atmosphäre dreht sich mit der Erde, analog wie das Wasser der Meere. Die Atmosphäre ist mit der Erde durch Reibung verbunden. Mit dem Weltraum entsteht keine Reibung, welche die Atmosphäre bremsen könnte.
2. Falsche Vorstellung von Trägeit. Die Trägheit bewirkt nicht, dass etwas träge ist, d.h. sich nicht bewegen will. Trägheit heisst nach Newton: Ein kräftefreier Körper bleibt in Ruhe oder bewegt sich geradlinig mit konstanter Geschwindigkeit. Das heisst hier, wenn die Atmosphäre einmal die Drehgeschwindigkeit der Erde hat, bleibt diese Geschwindigkeit erhalten, bis sie durch Kräfte verändert wird. Solchen Kräfte sind die Reibung mit der Oberfläche, Corioliskräfte und Druckunterschiede in der Atmosphäre, was zusammen Wetter und lokale Winde ergibt.
Erdkrümmung und Bauwesen
- 2) Warum müssen Ingenieure, Statiker und Architekten die Erdkrümmung nicht in ihren Berechnungen für z.B. Brückenkonstruktionen berücksichtigen?
Ich weiss nicht woher diese Behauptung stammt. Nur weil nicht alle grossen Bauwerke die Krümmung berücksichtigen müssen, heisst das nicht, dass sie nie berücksichtigt werden muss. Die haben wohl die falschen Leute gefragt.
Es hängt vom Bauwerk, seinem Zweck und seiner Grösse ab, ob die Krümmung berücksichtigt werden muss oder nicht. Es stimmt nicht, dass die Krümmung nie berücksichtigt wird. Teilchenbeschleuniger zum Beispiel müssen über grosse Distanzen exakt gerade sein. Die Krümmung wird beim Bau entsprechend berücksichtigt. Bei Eisenbahnen folgt man einfach der Erdkrümmung. Die Schienen sind flexibel genug, dass sie sich der leichten Krümmungen anpassen. Da muss die Krümmung nicht extra berücksichtigt werden, das passiert automatisch beim Verlegen der Geleise.
Bei grossen Brücken muss unter Umständen beim Bau, also beim Vermessen während des Baus mit Theodoliten, die Krümmung berücksichtigt werden. Je nach Bauart muss man dies jedoch nicht immer tun. Nehmen wir eine Hängebrücke: Die Pfeiler der Brücke werden einfach an ihrem Ort senkrecht gebaut. Dazwischen werden die Segmente in einem konstanten Abstand zur Wasseroberfläche aufgehängt. Und schon folgt die Brücke automatisch der Erdkrümmung, ohne dass diese extra berücksichtigt werden müsste. Bei der Planung wird natürlich schon berechnet, ob und wieviel die Krümmung Einfluss haben könnte. Eine Brücke muss aber schon seeehr gross sein, dass die Erdkrümmung einen Einfluss hat.
Bei einer langen Hängebrücke sind die Spitzen der Pfeiler wegen der Erdkrümmung weiter auseinander als deren Basis. Das wird aber oft überschätzt. Hier ist die Formel, wie der Abstand der Spitzen berechnet wird:
| (10) | |||||||||||||
| wobei' |
|
Beispiel: Die Pfeiler der Verrazano-Narrows Brücke sind 211 m hoch und sagenhafte 1298 m an der Basis voneinander entfernt. Das gibt an der Spitze der Pfeiler wegen der Erdkrümmung einen Abstand von:
Die Differenz zwischen Spitze und Basis ist somit nur gerade mal 43 mm! Beachte, dass die Strassensegmente nicht in Höhe der Spitzen liegen. Der Abstand wird entsprechend kleiner auf Strassenhöhe. Dieser kleine Abstand muss beim Bau nicht berücksichtigt werden, da die Toleranzen der Bauteile zusammen grösser sind.
Quelle: Structural Engineers: At what point does the curvature of the earth have to be factored in?; www.reddit.com
Erdkrümmung und Flugzeuge
- 3) Weshalb korrigieren Flugzeuge ihre Flugbahn nicht in kurzen Intervallen, um der postulierten Erdkrümmung folgen zu können? Die Fliehkraft von beschleunigten Flugzeugen müsste definitiv stärker sein als die angeblich auf sie wirkende "Gravitation" in höherem Abstand von der Erde...
1. Die Fliehkraft ist 300 mal kleiner als die Gravitation, trotz der hohen Tangentialgeschwindigkeit. Die Fliehkraft ist nicht bloss von der Geschwindigkeit abhängig, sondern auch vom Radius. Sie berechnet sich wiefolgt:
| (11) | ||||||||||
| wobei' |
|
Das ergibt für die Erde:
Die Gravitationsbeschleunigung ist g = 9,81 m/s2. Das ist fast 300 mal mehr!
Woher kommt die Vorstellung, man müsste von der Zentrifugalkraft bei 1668 km/h weggeschleudert werden? Wahrscheinlich daher: Wenn man ein Kinderkarussell mit 2,5 m Radius am Umfang mit 30 km/h antreibt, wie in einigen Youtube Videos zu sehen, dann werden die Insassen weggeschleudert. Was würde erst bei 1668 km/h passieren? Hier die Lösung des Rätsels: Nehmen wir ein Karussell mit 10 mal grösserem Radius, also 25 m, und gleicher Umfangsgeschwindigkeit. Das Karussell dreht sich nun 10 mal langsamer und die Zentrifugalkraft ist demenstprechend auch 10 mal kleiner. Vergrössern wir nun den Radius von 25 m auf 6 371 000 m. Trotz der Erhöhung der Umfanggeschwindigkeit von 30 km/h auf 1667 km/h resultiert nur eine sehr kleine Zentrifugalbeschleunigung, weil der immense Erdradius den Einfluss der höheren Umfangsgeschwindigkeit mehr als wett macht. Wer rechnen kann ist im Vorteil!
2. Flugzeuge korrigieren ihre Flugbahn kontinuierlich, nicht nur entlang der Erdkrümmung. Der (Auto-)Pilot korrigiert nicht in Intervallen. Das funktioniert so: Man will in einer bestimmten Höhe über Meeresgrund fliegen und diese Höhe konstant halten. Dazu trimmt man das Flugzeug einfach so, dass es diese Höhe einhält. In dieser Trimmung ist eine winzig, winzig kleine Auslenkung nach unten automatisch enthalten. Diese Auslenkung, um der Krümmung der Erde zu folgen, ist aber viel, viel kleiner als die Korrekturen, die durch Windeinflüsse notwendig sind. Der Pilot muss nicht bewusst die Erdkrümmung berücksichtigen. Daher wird nicht geschult, wie der Erdkrümmung gefolgt wird, sondern wie man die Höhe über Grund einhält. In dieser Hinsicht ist es nicht falsch zu sagen, der Pilot berücksichtigt die Erdkrümmung nicht. Er tut dies aber automatisch, indem er die Höhe konstant hält.
Die Korrektur wegen der Krümmung ist sehr minim. Sie berechnet sich wiefolgt:
| (12) | |||||||||||||
| wobei' |
|
Beispiel: Bei einer Fluggeschwindigkeit von v = 800 km/h und einer Flughöhe von 12 km ist die notwendige Korrektur 0,002°/s oder 0,12°/min. Jeder Windhauch benötigt eine viel grössere Korrektur.
Mir fällt auf, dass alle falschen Vorstellungen der Flat-Earther daher kommen, dass sie nicht in der Lage sind, die Grössenverhältnisse abzuschätzen oder zu berechnen.
Hätte ich einen Hut, so würde ich ihn ziehen.
Repekt für die saubere und detailierte Vorgehensweise.
Um so erschütternder sind manche der Antworten aus der Ecke der verblendeten Verschwörungsopfer. Leider scheinen sie zu glauben, dass Bildung Schmerzen bereitet.
Mach weiter so ....
ps: Das mit den Defizit, Grössenverhältnisse halbwegs einschätzen zu können, fällt mir auch regelmäßig auf. Zieht sich quer durch alle Diskussionen mit FEs.
Ein wirklich sehr gut recherchierter und detailierter Beitrag.
Es ist sogar einer der besten Texte, die ich bisher zu dem Thema gelesen habe.
Traurig ist nur, dass ein solcher Text im Jahr 2017 noch notwendig ist.
Es ist erschütternd, mit welcher Gewindigkeit das Wissen um grundlegende wissenschaftliche Fakten verloren geht.
Gerade die so genannten bildungsfernen Schichten scheinen in einer Welt zu leben, die mit unserer nicht s mehr zu tun hat und schlimer noch: sie scheinen darauf auch noch stolz zu sein.
Die Flach-Welt-Hypothese (denn zu einer Theorie fehlen leider grundlegende Voraussetzungen) kann keinerlei nachprüfbare Aussagen generieren. Je genauer man bei Flachweltlern nachfragt um so verschwommener und agressiver werden die Antworten. Früher oder später münden die wissenschaftlich begonnenen Diskussionen in Aussagen der Glaubenslehren.
Hallo Walter,
Du hast alles sehr gut argumentiert. Ich habe zwar keinen Theodoliten und die, von Dir empfohlene Theodolite App, kann auf meinem Android-Smartphone nicht installiert werden. So weit so schlecht. Also habe ich eine ähnliche App auf meinem Gerät installiert und auch ausprobiert. Zuerst habe ich aber festgestellt, dass es eine Abweichung zur Wasserwaage von +1,1° nach oben gab. Nun ja, es ist halt nur ein Handy und kein echter Theodolit im Preis von über 1000 Euro. Aber mir geht es eigentlich nur um die relative Werte. Aus verschieden Höhen vermessen, habe ich es tatsächlich festgestellt, dass der Horizont nicht auf Augenhöhe sei, also müsste die Erde eine kugelähnliche Form haben.
Eine Sache verstehe ich trotzdem nicht...
Wegen ihrer Länge habe ich die Fragen in meine Antworten unten kopiert - Walter Bislin
Hallo Maxfizios
Ich übernehme Deine Fragen hier in die Antworten, damit die Diskussion nicht zu lange wird.
Nicht-Sichtbarkeit von Lichtern auf der Nachseite der Erde auf Satellitenaufnahmen
Eine Sache verstehe ich trotzdem nicht: Auf den Bildern von der ISS sieht man, wie die Sterne leuchten und die Städte sind teilweise so hell, als würde nachts die Sonne darauf scheinen. Warum zeigt aber das Video des japanischen Wetter-Satelliten Himawari die Fullscan-Bilder in Echtfarben, die aber absolut nichts ähnliches zur NASA Bildern aufweisen? Es wird alles einfach nur schwarz dargestellt, wenn die Nacht einbricht, kein einziges helles Pixel ist zu erkennen, keine einzige Stadt, keine Spiegelung des Mondlichtes und auch keine Sterne. Die Bilder sollten doch eine Auflösung von bis zu 500 Metern pro Pixel erreichen? Wie ist das trotz der unterschiedlichen Entfernungen, Kamera Typen oder verwendeten Kanälen zu erklären?
Da spielen zwei Dinge eine Rolle: absolter Helligkeitsunterschied und Konstruktion der Kamera.
Die Kameras, die in der ISS verwendet werden, sind kommerzielle digitale Fotoapparate. In denen kann man Blende und Belichtung einstellen auf die Gesamthelligkeit einer Szene. Weil das menschliche Auge einen extrem grossen Helligkeitsbereich abdeckt, ist man oft erstaunt darüber, dass Kameras ihre Mühe mit Nachtaufnahmen haben. Aber die Helligkeitsunterschiede zwischen Tag und Nacht sind enorm!
Die Helligkeit von Objekten wie Sonne, Mond und Sterne werden technisch in Apparent Magnitude angegeben. Das ist ein logarithmischer Massstab, weil das Auge auch annähernd eine logarithmische Empfindlichkeit hat.
Hier die scheinbaren Helligkeiten verschiedener Objekte in Magnitudes:
- Sonne = -26.74
- Vollmond = -12.74
- ISS maximal von der Erde aus gesehen = -5.9
- Venus = -3.82
- Hellster Stern Sirius = -1.47
Der absolute Helligkeitsunterschied zwischen zwei Objekten, wie er für eine Kamera relevant ist, kann wiefolgt aus der Magnitude berechnet werden:
| (13) | |||||||
| wobei' |
|
- Sonne und Vollmond: 2,511926,74 − 12,74 = 398 137
- Vollmond und hellster Stern: 2,511912,74 − 1,47 = 32
Die Sonne ist also ca. 400 000 mal heller als der Vollmond.
Die Multispektralkamera des Himawari hat keine Blende und variable Verschlusszeit wie ein Fotoapparat, da er ja immer dasselbe Motiv aufnimmt. Da die Erde also mit derselben fixen Einstellung für Tag- und Nacht-Belichtung aufgenommen wird, es soll ja bei Halb-Erde die Tageshälfte nicht überbelichtet werden, wird die Nachtseite pitsch-schwarz. Kein Sensor kann solche Helligkeitsunterschiede im selben Bild ablichten.
Infos zur Multispektralkamera: Himawari-8/9 Imager (AHI); Meteorological Satellite Center (MSC) of JMA
Für Multispektralkameras ist das kein Problem, denn diese sind auch für Infrarot-Bereiche empfindlich. Nachtaufnahmen des Wetters macht man daher im Infrarotbereich. Das ergibt dann allerdings keine Echtfarbaufnahmen, da wir ja nicht Infrarot sehen können. Die Helligkeitsunterschiede im Infrarotbild werden daher einfach auf Farben im für uns sichtbaren Bereich abgebildet, was dann zu sog. Falschfarb-Bildern führt.
Bei Fotoapparaten und Filmkameras wird einfach die Blende maximal geöffnet und eine möglichst hohe Belichtungszeit eingestellt, sodass Bewegungen gerade noch nicht verschwimmen. Dass Städte auf dem Himawari-Bild nicht sichtbar sind, hat also damit zu tun, dass Städtebeleuchtungen aus der Luft gegenüber Tagesbelichtung von der Sonne zehn- bis hunderttausendfach schwächer sind. Dasselbe gilt für Sterne und Reflexionen des Mondes.
Probleme beim Messen der Rotation der Erde mit Gyroskopen
Ich, persönlich, finde aber viel wichtiger nicht die Frage, welche Form die Erde hat, sondern, ob sie sich überhaupt dreht? Denn, wenn die Erde wirklich eine sich (am Äquator) mit mehr als 1666 km/h ostwärts um die eigene Achse drehende Kugel wäre, wie kann man dann die folgenden Fragen beantworten?
Um die Erddrehung beweisen oder widerlegen zu können, muss man nur ein Gyroskop, Kurskreisel oder künstlichen Horizont zum Rotieren bringen und 15-60 min abwarten. Und genau das habe ich auch getan, ich habe ein von der offiziellen Wissenschaft anerkanntes Gerät nachgebaut, Dieses zeigte aber keinerlei Drift!
Warum kann ich keine scheinbare Drift sehen? Existiert sie tatsächlich?
Dein Nachbau ist zu wenig sensibel, d.h. die Reibungskräfte in den Lagern sind zu hoch um von der langsamen Erdrotation überwunden zu werden. Die scheinbare Drift existiert und muss in Heading Indicators bei Flugzeugen entsprechend alle 15-20 Minuten korrigiert werden.
Das Problem beim Messen der Erdrotation mit Hilfe von Kreiseln ist, dass selbst in der Aviatik verwendete mechanische Gyroskope nicht sensibel oder genau genug sind. Die allerkleinsten Ungleichgewichte und Reibungen in den Lagern (aufgrund der Erdrotation oder Bewegungen des Gerätes), Windströmungen oder Schwankungen im Antrieb erzeugen winzige Kräfte, die bewirken, dass der Kreisel wegdriftet. Nur ein schwerelos schwebender Kreisel behält seine Richtung bezüglich Fixsternen perfekt bei. Der Kreisel reagiert also durchaus auf Erdrotationen, wenn die Reibung in den Lagern der Aufhängung nicht zu gross ist und ihn mit der Erde koppelt, jedoch nicht wie gewünscht und kann daher nicht zur Messung der Erdrotation verwendet werden.
- Zitat: For example a typical Bendix King aircraft gyrocompass has a gyro drift rate of 20-30° per hour aus Intelligent Fibre-Optic Gyro (PDF); tritech.co.uk.
- Laut etlichen Quellen über Heading Indicators müssen diese alle 15 bis 20 Minuten neu ausgerichtet werden, wegen mechanischer und scheinbarer Drift (z.B. Flight Instruments: The Heading Indicator and Magnetic Compass; learntoflyblog.com).
- The instrument should be checked at least every 15 minutes during flight and reset to the correct heading. An error of no more than 3° in 15 minutes is acceptable for normal operations. Quelle: direction/heading indicator; pilotfriend.com
Es ist also anzunehmen, dass selbst bei in der Aviatik verwendeten Kreiseln die mechanische Drift in der Grössenordnung der Erdrotation ist.
Dazu kommt, dass viele Laien in ihren Experimenten gar nicht wissen, was der Kreisel eigentlich für Bewegungen vollführen sollte. Die einfache Vorstellung von 15 Grad horizontaler Rotation pro Stunde stimmt nur für die Pole. An allen anderen Orten der Erde würde sich der Kreisel in beiden Achsen bewegen, wenn die Reibung nicht wäre.
Ein anderes Problem ist, dass total unterschätzt wird, wie langsam sich die Erde dreht. Die langsamste Bewegung, die ein Flugzeug macht, ist der Flug im Kreis. Ein Kreis benötigt 2 Minuten bei einem Standard-Kreismanöver. Das heisst 180° pro Minute oder 10 800° pro Stunde. Die Erde dreht sich mit 15° pro Stunde. Das ist 720 mal langsamer! In der Praxis macht ein Flugzeug viel schnellere Drehungen bei Manövern. Zum Beispiel dauert ein 360° Looping nur einige Sekunden. Ein Gyroskop, das nicht am Pol ist, würde sich noch langsamer als 15° pro Stunde drehen (15 · sin( Breitengrad )). Da ist es kein Wunder, dass ein Instrument, das schnelle Drehungen noch akkurat anzeigen kann, bei so langsamen Drehungen wie der Erdrotation versagen muss.
Die Probleme mit mechanischen Kreiseln werden in der Aviatik auf verschiedene Weise umgangen - man will ja nicht die Rotation der Erde messen, daher ist das möglich:
Auf die komplizierten Gyroskope in früheren INS (inertial reference system) kann ich nicht im Detail eingehen, das sprengt den Rahmen dieser Diskussion. Aber unter Prinzip eines Gyrocompasses kannst du in etwa nachlesen, wie Aufwändig solche Systeme sind. Neue Gyroskope in Flugzeugen sind sog. Laser-Gyroskope, also rein optische Instrumente.
In einem künstlichen Horizont (Attitude Indicator AI) wird die kurzzeitige Stabilität des Kreisels ausgenutzt, um grössere Bewegungen des Flugzeugs zu messen und anzuzeigen. Da auch diese Kreisel driften, werden sie über einen speziellen Mechanismus, sog. pendulous vanes (siehe How are attitude indicators kept accurate?) kontinuierlich bezüglich der Gravitation aufgerichtet. Diese Aufrichtung erfolgt mit einer Geschwindigkeit von ca. 3-5 Grad pro Minute. Würde ein Flugzeug längere Zeit im Kreis fliegen, würde dieses Instrument mit der Zeit sich auf die falsche Beschleunigung aus Gravitation und Zentrifugalbeschleunigung einstellen. Diese Eigenheit muss einem Piloten bekannt sein, sodass er sich in solchen Flugmanövern nicht alleine auf dieses Instrument verlässt.
Mechanische Kreiselkompasse, wie sie in kleinen Flugzeugen vorkommen, muss man in regelmässigen Abständen von Hand neu nach dem magnetischen Nordpol ausrichten. Dazu gibt es einen Drehkonpf am Gerät.
- Demonstration of an Aircraft Attitude Indicator (AI) self erection
- Time lapse of self erecting aircraft gyroscope in an AI
Prinzip eines Gyrocompasses
Mechanische Kreiselkompasse in Schiffen nutzen eine andere Eigenheit von Kreiseln aus:
"A gyrocompass is a type of non-magnetic compass which is based on a fast-spinning disc (gyroscope) and the rotation of the Earth to find geographical direction automatically" (Quelle: Wikipedia). Zu deutsch: Ein Gyrokompass ist ein nicht-magnetischer Kompass auf Basis einer schnell rotierenden Scheibe (Gyroskop) und der Rotation der Erde, um die geografische Richtung der Erdachse automatisch zu finden.
Einige Beschreibungen findendest du in den Quellangaben der Wikipedia, z.B. diese (englisch):
A. THEORY OF THE GYROCOMPASS; GYROCOMPASS, AUXILIARY GYROCOMPASS, AND DEAD RECKONING ANALYZING INDICATOR AND TRACER SYSTEMS; San Francisco Maritime National Park Association.
Oder hier ein sehr gutes YouTube-Video dazu: Design of the Sperry Mk XIV Gyro-Compass.
Wenn man die Kreiselachse horizontal bezüglich Erdoberfläche anlegt und in dieser Ebene fixiert, sodass er sich nur in der vertikalen Achse drehen kann, entstehen durch die Erdrotation Kräfte, welche den Kreisel so präzessieren lassen, dass er sich nach Norden ausrichtet. Wird ein solcher Kreisel gestartet, richtet er sich in 1-2 Stunden selbständig nach Norden aus. Diese Zeit kann verkürzt werden, indem man ihn vorher ungefähr nach Norden ausrichtet.
Aber auch diese Kreisel müssen mit den Reibungskräften kämpfen. Diese wirken sich hier in einer konstanten Abweichung gegenüber Norden aus. Solche Kreisel sind so konstruiert, dass sie an dünnen Drähten aufgehängt sind. Die Gymbal-Achsen werden nicht durch den Kreisel selbst bewegt, sondern durch Motoren. Die kleinste Tendenz des Kreisels, sich drehen zu wollen, wird über Sensoren gemessen und ein Motor dreht dann die Aufhängung so, dass sie dem Kreisel folgt. Mit dieser Motor-getriebenen Aufhängung ist die Kompassanzeige gekoppelt.
Vermutlich kannst du es vergessen, mit einem herkömmlichen mechanischen Kreisel die Erdrotation messen zu wollen. Du kannst allenfalls mit einem in Wasser schwimmenden, horizontal gefixten Kreisel die Tendenz, sich nach Norden ausrichten zu wollen, feststellen. Diese Bewegung ist jedoch sehr langsam und die leichtesten Windströmungen sind stark genug, diese Tendenz zu beeinflussen und zu verfälschen. Da ein Kreisel selbst Windströmungen verursacht, müsste man diese Störgrössen durch entsprechende Baumassnahmen abschirmen, stabilisieren, vermessen und kompensieren, wie es in den Schiffskompassen gemacht wird.
Im folgenden Video siehst du einen teilweise erfolgreichen Versuch nach diesem Prinzip: Gyrocompass Follow-up: Testing the Constant Torque Hypothesis von GarbageGamer74.
Ich kann bei meinem Gyro die Drehzahl jederzeit verändern, dabei ändert sich sofort die Lage des Kreisels!
Selbstverständlich. Bei einer Änderung der Drehzahl wird ein Drehmoment auf den Kreisel ausgeübt, das dessen Drehzahl ändert. Ein solches Drehmoment ist eine externe Kraft, die den Kreisel präzessieren lässt. Schon daran siehst du, dass kleinste Ungenauigkeiten auch beim Antrieb einen grossen Einfluss auf den Kreisel haben.
Foucault-Pendel Aufbau
Foucaultsches Pendel ist für mich kein Beweis, weil seine Amplitude mit der Zeit ebenso kleiner wird, ansonsten muss man es z.B. mit einem Elektromagneten antreiben, dabei würden aber Störungen im System entstehen, die für das Entstehen des bekannten Musters verantwortlich wären.
Es gibt eine verblüffend einfache mechanische Konstruktion um seitliche Auslenkungen wirkungsvoll zu dämpfen: man nennt es den Charron Ring nach seinem Erfinder. Es ist ein Ring, der oben unterhalb der Pendelaufhängung montiert wird. Das Pendel stösst bei der grössten Auslenkung an diesen Ring. Wenn das Pendel leicht seitlich schwingt, entsteht durch das mehr seitliche Anstossen an dem Ring eine kleine Kraft in die seitliche Gegenrichtung, die diese seitliche Auslenkung dämpft bis sie verschwindet.
Wenn das Pendel nicht sehr exakt gebaut ist und somit diese Dämpfung am Ring häufig auftritt, wird das Pendel durch die kurzzeitige Reibung am Ring leicht mit der Erdrotation mitgeführt. Das Pendel rotiert dadurch etwas langsamer als die Erdrotation. Aber die Genauigkeit solcher Pendel ist im Bereich von wenigen Prozent oder besser.
Bauanleitung für Schule, magnetische Anregung, Charron Ring zur Dämpfung der Querschwingung
Hallo Walter,
Du hast u.a. folgendes geschrieben: „Das Problem beim Messen der Erdrotation mit Hilfe von Kreiseln ist, dass selbst in der Aviatik verwendete mechanische Gyroskope nicht sensibel oder genau genug sind.“
Das ist nur eine Annahme, so was kann leicht überprüft werden, indem man nur ein Gyroskop auf einen Drehteller stellt, der eine Umdrehung in 24h macht. Würde sich das Gerät dabei mitdrehen, dann wäre es tatsächlich nicht sensibel genug. Sollte der Kreisel aber eine Drehbewegung anzeigen, im Idealfall wären das 15°/h, dann würde es bedeuten, dass es die Erde ist, die still steht.
Wäre so ein Selbsttest für dich kein eindeutiger Beweis?
Das Beste ist, dass so ein Experiment jemand schon mal gemacht hat, hier ist der Link zur einer 20 Min. Zusammenfassung:
https://www.youtube.com/
Übrigens, ich fand es nicht besonders nett, dass du mein Kommentar so dermaßen zensiert hast, dass sogar harmlose Wikipedia-Links zum Kurskreisel und Kreiseldrift gelöscht wurden.
MfG
Max
Hallo Max, sorry wegen dem Löschen der Links. Es hat nichts mit Zensur zu tun. Ich will einfach die Länge der Kommentare nicht überborden lassen und beim Thema des Artikels bleiben. In diesem Beitrag geht es um die Krümmung der Erde, nicht um deren Rotation. Daher bitte ich Dich, keine weiteren Kommentare zu Kreiseln hier zu posten. Ich bin bereit in Emails darauf einzugehen.
Also hier nochmals Deine Links:
- https://www.youtube.com/
watch? -> Hier wird ein echter Flugzeug-Kurskreisel getestet. Leider sieht man in dem Video gar keine Drift, wahrscheinlich wurde das Gerät so manipuliert, dass man gar keine Drift sehen könnte, zumindest im Uhrzeigesinn nicht. Übrigens, der Mann in dem Video hatte auch einen Foucaultschen Kreisel nachgebaut, und Dieser war auch zum Schluss abgedriftet. Das war aber nicht wegen der Erdrotation passiert, sondern weil seine Drehzahl sich kontinuierlich verringerte.v=nUFMZkxochs - https://de.wikipedia.org/
wiki/ Kurskreisel - https://de.wikipedia.org/
wiki/ Kreiseldrift
Nachweisen der Erdrotation mit Kreiseln
- Das ist nur eine Annahme, so was kann leicht überprüft werden, indem man nur ein Gyroskop auf einen Drehteller stellt, der eine Umdrehung in 24h macht. Würde sich das Gerät dabei mitdrehen, dann wäre es tatsächlich nicht sensibel genug. Sollte der Kreisel aber eine Drehbewegung anzeigen, im Idealfall wären das 15°/h, dann würde es bedeuten, dass es die Erde ist, die still steht.
Deine Idee ist theoretisch korrekt. Aber es gibt keine idealen Kreisel. Daher kann man auch nicht eindeutige Versuche für oder gegen die Rotation der Erde auf diese Weise machen. Selbst wenn die Erde still stehen würde, würde ein realer Kreisel nicht einfach eine fixe Ausrichtung im Raum anzeigen, denn die kleinsten Ungleichgewichte und Reibungen würden ihn wegdriften lassen, was als eine Rotation der Erde interpretiert werden könnte.
Es kann nur überprüft werden, ob die Mechanik des Kreisels genau genug ist, wenn man genau weiss, was der Kreisel für eine Bewegung ausführen sollte. Die verbreitete Vorstellung, dass ein Kreisel eine Drehung von 15°/h in der horizontalen Ebene machen sollte, ist falsch. Dies gilt nur an den Polen. Überall sonst ist es eine Kombination von horizontaler und vertikaler Drehung, abhängig vom Breitengrad. Zum Beispiel sollte jeder parallel zur Drehachse der Erde ausgerichtete Kreisel keinerlei Bewegung zeigen, ob sich die Erde dreht oder nicht! Wenn man nun einen Kreisel auf einen Drehteller stellt, muss man diese Drehung zusätzlich berücksichtigen.
Die Kunst beim Bau eines Kreiselinstrumentes
Es gibt keine idealen frei schwebenden Kreisel. Alle Kreisel auf der Erde müssen irgendwie gelagert sein. Reibungen, Ungleichgewichte, ungleiche Reibung in den Lagern des Kreisels, Magnetfelder, Windströmungen usw. üben Drehmomente auf den Kreisel aus und bewirken eine Präzession desselben. Je grösser die Störungen, umso grösser die Präzession. Je massereicher der Kreisel (grosses Trägheitsmoment) und schneller der Kreisel rotiert, umso kleiner die Präzession. Sind die Lagerkräfte der Gymbals zu gross, kann der Kreisel nicht frei präzessieren, sondern wird vom Gybal in eine äussere Bewegung gezwungen.
Man kann keine idealen Kreisel bauen. Die Kunst beim Bau eines Kreiselinstrumentes ist es daher, die Reibungen und Unsymmetrien so klein zu halten, dass die Präzession des Kreisels für den gewünschten Anwendungszweck klein genug ist. Oder dass die Präzession durch andere konstruktive Massnahmen wie den Pendulum Vanes von künstlichen Horizonten korrigiert wird.
Wie gesagt, ich denke nicht, dass ein einfacher mechanischer Flugkreisel genau genug ist, geschweige denn so ein "hochpäziser" Spielzeugkreisel wie im Video. Der Hersteller gibt selbst zu, dass dieser Kreisel die Erdrotation nicht nachweisen kann. Ich erwarte, dass beim Spielzeugkreisel die Reibung der Gymbal-Lager so gross ist, dass sich der Kreisel einfach mit dem Teller dreht. Von einem guten Flugzeugkreisel erwarte ich, dass dieser aufgrund der kleinen Drehmomente, die von der Rotation des Tellers und der Erde über die Gymbal auf den Kreisel ausgeübt werden, in irgend welche unvorhersagbaren Richtungen wegdriftet, abhängig auch von der Ausgangsausrichtung.
Häufige Fehler bei Gyro-Versuchen
Ich kenne das von dir verlinkte Video. Es zeigt typisch, dass die Versuchsperson keine Ahnung hat, was sie da eigentlich tut und erwarten kann. Einige auffällige Punkte sind:
- Das Gyro ist in einem Versuch mit einem Kabel mit den externen Batterien verbunden. Das Kabel bewirkt relativ grosse externe Kräfte. Das ist nicht tolerabel für so sensible Versuche. Ein Kreisel mit sehr wenig Reibung würde bei der kleinsten Bewegung der Auflage in verschiedene Richtungen wegdriften aufgrund der Kräfte des Kabels, Windströmungen usw. Tut es aber nicht, was zeigt, dass die Kraft des Kabels den Kreisel auf seiner Position fixiert, und nicht die Achsstabilität des Kreisels.
- Der Kreisel ist definitiv nicht ausbalanciert und die Reibung in den Lagern ist viel zu gross. In den Versuchen mit angeflanschten Batterien ist der Schwerpunkt des Gymbals weit unterhalb der horizontalen Drehachse. Das ist nicht ausbalanciert! Der Kreisel kann sich so nicht frei bewegen. Eine solche Konfiguration mit sehr kleinen Lagerreibungen würde sicherlich wegdriften. Ein Drehmoment von so einer Inbalance muss eine Präzession bewirken, was sie hier aber nicht tut. Folglich sind die Reibungen in den Lagern viel zu gross.
- Ich bin sicher, wenn die Versuchsperson den Kreisel auf dem Drehteller nicht mit einem externen Kabel verbunden hätte, würde sich der Kreisel mit dem Teller drehen, als ob alle Lager fixiert wären. Wenn man genau hinschaut, sieht man in den Zeitraffer-Aufnahmen, dass der Kreisel versucht, sich mit dem Teller zu drehen aber immer wieder vom Kabel in die bezüglich Umgebung fixe Position zurückgeschubst wird.
- Die Versuchsperson versucht mit schnellen Bewegungen des Tisches zu beweisen, dass der Kreisel sich frei bewegen kann und tatsächlich seine Richtung im Raum beibehält, dass also der Kreisel perfekt funktioniert. Er vergisst dabei, dass schnelle Bewegungen grosse Drehmomente erzeugen, welche die statische Reibung in den Lagern überwinden. Zudem sieht man, dass der Kreisel selbst jetzt nicht seine Richtung im Raum beibehält, sondern versucht in der Nickachse auszuweichen oder sogar etwas in der horizontalen Achse mitdreht. Eindeutige Zeichen für viel zu grosse Reibungen in den Lagern. Schnelle Bewegungen sind kein Beweis für die Genauigkeit eines Kreiselinstrumentes. Das ist ja gerade der Witz bei den Flugzeugkreiseln. Schnelle Bewegungen des Flugzeugs, so um mindestens 180°/min, zeigen diese Instrumente genau genug an. Aber so langsame Bewegungen wie die Rotation der Erde erzeugen Effekte, die schwächer sind als die Drift aufgrund der Reibung und Ungleichgewichte des Gyros. Man kann daher von diesen Instrumenten keine präzisen Messungen von Rotation erwarten.
Bitte verstehe folgendes: Nur ein frei schwebender Kreisel behält seine Richtung im Raum bei. Jede noch so kleine Kraft, die auf diesen Kreisel einwirkt, bewirkt sofort eine Präzession. Eine solche Kraft kann von einem Gymbal auf den Kreisel ausgeführt werden. Es reicht aber auch schon die vom Kreisel selbst erzeugte Windströmung. Oder das Magnetfeld der Erde kann schon ein konstantes Moment auf den Kreisel oder seinen Antrieb ausüben. Daher sind professionelle hochpräzise Kreisel in einem Vakuumgehäuse magnetisch abgeschirmt verpackt. Unsymmetrien in der Lagerreibung bewirken Drehmomente, die den Kreisel präzessieren lassen. Bewegungen des Gymbals, aufgrund der Rotation der Erde, bewirken über die Lagerreibungen Drehmomente auf den Kreisel, welche diesen driften lassen.
Um die Erdrotation präzise messen zu können, müssen alle diese Einflüsse genau bekannt sein und so klein gemacht werden, dass deren Auswirkung wesentlich kleiner sind, als die zu messende Rotation der Erde. Das ist nur mit elektronisch unterstützten oder sehr Massereichen System mit extrem kleinen Reibungen möglich.
Besser messen kann man die Tendenz eines Gyros, das in der horizonalen Achse gefixt ist, sich nach Norden ausrichten zu wollen. Das ist das Prinzip des Kreiselkompass. Im Versuch von:
Gyrocompass Follow-up: Testing the Constant Torque Hypothesis von GarbageGamer74.
ist es gelungen, die Reibung der Vertikalachse durch Wasserlagerung so zu minimieren und die magnetischen Einflüsse so zu kompensieren, dass sie kleiner sind als der Effekt der Erdrotation. Die Versuche zeigen zwar noch kleine konstante Abweichungen aufgrund des Einflusses des Magnetfeldes der Erde, aber die Tendenz der Nordsausrichtung ist eindeutig und repetierbar sichtbar. Die Erde rotiert!
Hi,
da dir Refraktion so wichtig ist. Was sagst du zu diesem Video?
https://www.youtube.com/
was mich aber immer ärgert ist .. wenn jemand sich hinter mathematik versteckt .. um mir
klar machen zu wollen .. das ich zu dumm bin und ich offenbar nicht in der lage bin .. das .. was meine augen mir senden .. ordentlich zu prozessieren zu können .. wie z.b. evtl. refraktion nicht mit einbeziehen zu können! aber richtig ätzend wird es .. wenn man zum beweis eines klar bestimmbaren fakts wie der erdgröße und krümmung .. einen gummi-konstante herranzieht wie die refraktion .. und diese dann noch zu einer art totschlag keule hochstilisieren möchte .. da ja kein flacherdler an so krasse sachen überhaupt denkt! immerhin können flacherdler einfach nicht einschätzen wie groß die distanzen auf der erde sind und so!
weisste .. ich bin vor mir aus jetzt echt assi .. wie ich hier daher rede .. aber dein aroganz und alle leute die sich für das thema flache erde interessieren .. durch die blumen als trottel zu diffarmieren .. ist einfach schrecklich und verdient halt nicht viel respekt.
aber der abschuss sind die fotos deren echtheit du einfach mal selber hoch amtlich beglaubigst .. ein foto aus einem klar seitlich geneigten flugzeug das beweisen soll das der horizon nicht "eye level" sei oder das lustig nasa bild mit den nordlichtern und sternen im hintergrund. und das wo die nasa sich ja kaum drauf einigen kann ob jetzt deren digi cams jetzt nun sterne im hintergrund aufnehmen können oder nicht.
Unsere Sinne lassen sich täuschen:
- selective attention test (invisible gorilla)
- The Monkey Business Illusion
- Test Your Awareness : Whodunnit?
Wenn ich wissen will, ob die Erde flach oder kugelförmig ist, dann muss ich erst einmal wissen, woran ich den Unterschied erkennen kann. Dazu machte ich die App auf dieser Seite, basierend auf mathematischen Modellen der flachen und kugelförmigen Erde, mit denen ich berechnen kann, wie es für uns Winzlinge aussehen müsste, auf der flachen oder kugelförmigen Erde zu leben. Ich kann nun Bilder der Realität mit Vorhersagen beider Modelle vergleichen um herauszufinden, welches richtig oder falsch ist. Ich kann mit den Modellen herausfinden, wie man die Unterschiede gut erkennen kann und ensprechend nach diesen in der Realität suchen.
Ob der Horizont wirklich auf Eye-Level ist lässt sich mit einfachen Mitteln überprüfen und die Krümmung lässt sich gut mit Superzoom erkennen:
- Horizon Drop at Varying Altitudes. Flat Earth Debunked.
- Soundly Proving the Curvature of the Earth at Lake Pontchartrain
Betreff Satellitenbilder:
- Das Wahre Gesicht der Erde, Kameradistanz spielt eine Rolle
- Echtfarb-Aufnahmen der Erde vom Satelliten Himawari der JMA
- Können wir die Abplattung der Erde in Satellitenbildern sehen?
Phantastische Arbeit! Vielen Dank!
Ist nicht der von der Nordhalbkugel zu sehende, scheinbar "ruhende" Polarstern ein simpler Beweis für die Drehung der Erde? Schließlich "ruht" der Polarstern ja nur scheinbar, da die Rotationsachse der Erde momentan zufällig auf ihn zeigt.
Super Arbeit Herr Bislins!
Ich arbeite gerade an einem Referat zum Thema flache Erde und ihr Seite hat mir sehr geholfen.
Vielen Dank für ihr tolle Recherche und guten Erklärungen!
mit freundlichen Grüßen
Jannes Lucht
Schritt 2: Polarstern zur Bestimmung des Breitengrades
Wie in meinem letzten Post bereits angemerkt, die Drehachse der Erde ist zufällig auf den Polarstern ausgerichtet und damit ihr geographischer Nordpol. Auf einer kugelförmigen Erde ist es (auf der Nordhalbkugel) nun einfach möglich Breitengrade zu messen, weil die Höhe des Polarsterns über dem Horizont durch die Erdkrümmung zum Äquator hin abnimmt, zum geographischen Nordpol hin zunimmt. So etwas geht nur auf einer kugelförmigen Erde.
Wäre die Erde eine Kugel, würden wir Sternschnuppen aus allen möglichen Richtungen aus dem "3-D Weltall" in unsere Atmosphäre eindringen sehen. Da sie jedesmal Richtung des Horizonts fallen, beweist eindeutig, dass die Erde flach ist!
Ansonsten würden wir kreuz und quer fliegende Meteoriten sehen.
REAL EYES
REALIZE
REAL LIES
EARTH IS FLAT, SPACE, CURVATURE AND SATELLITES DON'T EXIST!
Funkybrain: Wäre die Erde eine Kugel, würden wir Sternschnuppen aus allen möglichen Richtungen aus dem "3-D Weltall" in unsere Atmosphäre eindringen sehen. Da sie jedesmal Richtung des Horizonts fallen, beweist eindeutig, dass die Erde flach ist!
Du hast nicht verstanden was Sternschnuppen sind, woher sie kommen und wie sie in die Atmosphäre eindringen. Und deshalb ist die Erde flach? Was ist denn das für eine Schlussfolgerung?
Im Gegenteil: Meteoritenströme haben ihre Ursache im heliozentrischen System!
Weshalb kommen Sternschnuppen alle aus einer bestimmten Stelle am Himmel?
Zitat: "Das liegt an der Flugrichtung der kugelförmigen Erde. Die Staubteilchen treffen als erstes auf die Stelle der Lufthülle, die vorneweg fliegt. Sternschnuppenschwärme werden nach dem Sternbild benannt, aus dem sie alle zu kommen scheinen. An den Sternbildnamen wird einfach die Nachsilbe '-iden' angehängt. So weiß man dann auch, in welche Richtung man schauen muss, wenn man sie entdecken möchte." Quelle: astrokramkiste.de
- Siehe auch: Die wichtigsten Meteorströme; timeanddate.de
- Wikipedia: Meteor, insbesondere Meteorströme
Würde sich die Erde mit 107 000 km/h um die Sonne drehen, würden wir doch nicht nur die 64 mal langsamere Bewegung um den Polaris erkennen sonder müssten eigentlich sehen, wie die Sterne sich horizontal Bewegen würden. Die befinden sich seit tausenden von Jahren am selben Platz. Habe in verschiedenen Astronomie Apps getestet, dass in 3 000 Jahren Polaris sich nicht um ein My bewegt!
Zudem wie stellt ihr euch vor, dass sich eine Wasser Oberfläche der Form des Grundes anpasst? Das ist der Denkfehler den ihr macht! Wasseroberfläche ruhenden ist immer horizontal und kann nicht gewölbt sein auch nicht auf eine grossen Erde! Auf einer Kugel geht der Boden unter den Füßen in alle Richtungen gleichmäßig nach unten. D.h. an einem Strand dürfte es gar kein Wasser zu deinen Füßen haben wenn du ins Meer raus schaust, denn der Boden wölbt sich vor dir nach unten weg und seit Wasser vom Berg ins Tal fließt... müsste es ja den Berg runter fließen (Fake Gravitation hin oder her).
Gravitation: stark genug Weltmeere (unvorstellbare Menge und daher Gewicht an Kubikmetern Wasser) vom Einfluss der Erddrehung und der Rotation um die Sonne aud der Erde zu halten, aber nicht stark genug um einen Vogel am Boden zu halten?
ppl wake up, it's time!
Gut dass wir darüber angefangen haben zu sprechen...
Eigenbewegung von Sternen
unbekannt: Würde sich die Erde mit 107 000 km/h um die Sonne drehen, würden wir doch nicht nur die 64 mal langsamere Bewegung um den Polaris erkennen sonder müssten eigentlich sehen, wie die Sterne sich horizontal Bewegen würden. Die befinden sich seit tausenden von Jahren am selben Platz. Habe in verschiedenen Astronomie Apps getestet, dass in 3000 Jahren Polaris sich nicht um ein My bewegt!
Falsch, die Sterne bewegen sich schon. Allerdings ist diese Bewegung extrem klein, noch kleiner als du angenommen hast, wie ich nachfolgend zeige:
Die Eigenbewegung der Sterne wird in Bogensekunden pro Jahr angegeben ("/a). Der nächste Stern Proxima Centauri ist etwa 4,01 ·1013 km (4,24 Lichtjahre) von uns entfernt und er bewegt sich erst noch in etwa derselben Richtung mit vergleichbarer Geschwindigkeit durch die Milchstrasse wie wir. Dieser Stern ist also etwa 268 000 mal weiter entfernt als unsere Sonne. Aber nehmen wir mal an, dieser Stern bewege sich nicht mit unserer Sonne, sodass die Relativgeschwindigkeit von uns bezüglich dieses Sterns 107 000 km/h sei. Wieviel müsste sich dieser Stern von uns aus gesehen bewegen?
Dazu berechnen wir den Winkel, um den sich dieser Stern am Himmel während eines Jahres bewegt. Wir nehmen eine relative Geschwindigkeit bezüglich unseres Sonnesystems von 107 000 km/h an. Rechnen wir den Weg aus, den der Stern in einem Jahr zurücklegt: s = 107 000 km/h · (365,25·24 h) = 938 000 000 km. Diese Distanz ergibt von uns aus gesehen einen Winkel von:
| (14) |
Kannst du eine Bewegung eines Sterns um weniger als 5 Bogensekunden pro Jahr sehen? Sicherlich nicht. Der Stern mit der höchsten bislang gemessenen Eigenbewegung ist Barnards Pfeilstern, der sich mit 10,34 Bogensekunden pro Jahr bewegt und nur sechs Lichtjahre von der Erde entfernt ist. Das heisst es vergehen 348 Jahre bis sich dieser Stern nur um 1 Grad am Himmel bewegt hat. Und das ist der weitaus schnellste Stern. Die meisten Sterne bewegen sich mit unserer Sonne parallel um die Milchstrasse und sind wesentlich weiter entfernt. Es dauert Jahrtausende bis sich diese Sterne um einen Bruchteil eines Grades am Himmel bewegt haben.
Solche kleinen Winkel kann man jedoch messen und daraus die Entfernung und Eigenbewegung für Sterne bis ein paar 100 Lichtjahre Entfernung berechnen.
Eine wesentlich grössere Bewegung, die alle Sterne gleichsam betrifft, entsteht durch die Präzession der gegenüber der Sonnenumlaufbahn um 23,43° geneigten Erdachse. Diese Achse rotiert ca. einmal in 26 000 Jahren, sodass sich die Position aller Sterne in 13 000 Jahren um 46,86° verschiebt. Alle Sterne rotieren um eine Achse die senkrecht auf der Erdumlaufbahn steht.
Diese Bewegung muss beim Ausrichten von Teleskopen berücksichtigt werden. In den dazu vorhandenen Polsuchern ist eine Grafik eingraviert, mit welcher der Polarstern je nach Jahr eingestellt werden kann, siehe Skywatcher HM6 Polsucher.
Wasser auf der Erdkugel
unbekannt: Zudem wie stellt ihr euch vor, dass sich eine Wasser Oberfläche der Form des Grundes anpasst? Das ist der Denkfehler den ihr macht! Wasseroberfläche ruhenden ist immer horizontal und kann nicht gewölbt sein auch nicht auf eine grossen Erde!
Du machst einen Denkfehler: du meinst dass überall auf der Erde Unten parallel zur Erdachse Richtung Süden ist. Das ist nicht der Fall. Da ist kein Gravitationsfeld ausserhalb der Erde, welches alles in Südrichtung zieht. Das Gravitationsfeld der Erde zeigt ins Zentrum der Erde. So ist an jeder Stelle der Erde Unten die Richtung zum Erdzentrum hin. Wenn du am Äquator auf einem Podest stehst und von dort runter springst, wirst du in Richtung Zentrum der Erde fallen. Und weil die Richtung, wohin du fällst immer Unten ist, ist am Äquator Unten nicht in Richtung Süden, sondern zur Erdmitte hin, wie überall auf dem Globus. Vergiss die Vorstellung deines Globus auf dem Tisch, der von einer externen Schwerkraft als ganzes nach unten gezogen wird. Für die Erde gibt es diese externe Schwerkraft nicht. Also gibt es auch kein externes Unten. Es gibt nur ein Unten zum Zentrum der Erde hin.
Nun zum Wasser. Du kannst dir das Gravitationsfeld der Erde in Schichten je gleicher Stärke um die Erde vorstellen. Höhere (weiter vom Zentrum entfernte) Schichten entsprechen einer höheren potentiellen Energie. Wasser sucht sich immer die Ebene mit der tiefst möglichen potentiellen Energie. Da alle Schichten mit derselben potentiellen Energie kugelförmig um die Erde liegen, muss das Wasser diese Kugelform annehmen, wenn es sich überall auf derselben äquipotentiellen Schicht befindet. Wenn das Wasser nicht überall auf derselben äquipotentiellen Schicht liegt, entstehen dadurch seitliche Kräfte, die das Wasser in Richtung niedrigerer Schichten fliessen lassen, solange bis das Wasser auf dem ganzen Planeten auf derselben äquipotentiellen Schicht liegt und somit keine seitlichen Kräfe mehr auftreten.
Hier ist ein Video, das zeigt, wie eine magnetische Flüssigkeit sich auf äquipotentiellen Schichten um einen magnetischen Körper krümmt und seine Form annimmt. Das selbe Prinzip wie beim Wasser auf der Erde unter ihrer Schwerkraft. Der Unterschied ist, dass das Magnetfeld zwei Pole hat und die magnetische Flüssigkeit auch mit sich selbst interagiert (bildet kleine Ausbuchtungen). Aber das Grundprinzip ist vergleichbar: Levitating Magnetic Fluid; JD Rock's Youtube Kanal
Gravitation, Wasser und Vögel
unbekannt: Gravitation: stark genug Weltmeere (unvorstellbare Menge und daher Gewicht an Kubikmetern Wasser) vom Einfluss der Erddrehung und der Rotation um die Sonne aud der Erde zu halten, aber nicht stark genug um einen Vogel am Boden zu halten?
Du hast offenbar keine Ahnung wie Gravitation zwischen Objekten wirkt. Die Gravitationskraft zwischen zwei Körpern ist abhängig von der Masse beider Körper und deren Abstand:
| (15) | ||||||||||||||||
| wobei' |
|
Der blaue Teil der Formel ist für alle Objekte auf der Erdoberfläche gleich gross. Die Anziehungskraft auf ein Objekt ist dort nur noch von der Masse m des Objektes abhängig.
Ein Liter Wasser hat eine Masse von m = 1 kg. Er wird von der Erde nach Formel (15) mit einer Kraft von etwa 10 N (N = Newton) angezogen. Wenn wir die Anziehungskraft auf das Wasser aller Ozeane berechnen wollen, müssen wir diese Kraft mit 1,38 ·1021 (Anzahl Liter Wasser auf der Erde) multiplizieren. Alle Ozeane werden somit mit einer Kraft von 1,38 ·1022 N von der Erde angezogen. Diese immense Kraft ist bei weitem genug, dass das alles Wasser auf der Erdoberfläche bleibt.
Ein Schmetterling hingegen hat ein Gewicht von sagen wir ein paar Gramm. Die auf ihn wirkende Anziehungskraft ist entsprechend nur ein paar Milli Newton. Diese Kraft ist so klein, dass sich der Schmetterling problemlos mit seinen Flügeln an der Luft in die Höhe stossen kann.
Die Gravitationskraft ist also nicht für alle Objekte gleich gross, sondern hängt von deren Masse ab. Wenn wir einen Gravitations-Versuch im Labor machen wollen, wo zwei Massen nur ein paar kg schwer sind, entstehen nach der Formel (15) nur winzige Kräfte zwischen diesen Massen. Entsprechende Versuche sind nicht einfach anzustellen, siehe Cavendish Experiment.