WaBis

walter.bislins.ch

Rainy Lake Experiment: Formeln

Diese Seite enthält die Herleitung der meisten Formeln, die im Rainy Lake Experiment verwendet wurden.

Terrestrial Refraktion

Siehe Deriving Equations for Atmospheric Refraction, um zu erfahren, wie die terrestrische atmosphärische Refraktion aus grundlegenden physikalischen Gesetzen hergeleitet werden kann und wie die Gleichungen und Konstanten abgeleitet werden, die in Formeln zur Berechnung der Refraktion verwendet werden.

Radius of the Earth

Siehe Method to calculate the Radius of the Earth from 3 Points um zu erfahren wie die App zur Visualisierung der GNSS-Daten den Erdradius anhand von 3 GPS-Vektoren berechnet.

Koordinaten-Transformationen

Siehe WGS84 Koordinatensystem um zu erfahren wie Vektoren zwischen kartesischen ECEF-Koordinaten und geodätischen Ellipsoid-Koordinaten transformiert werden können.

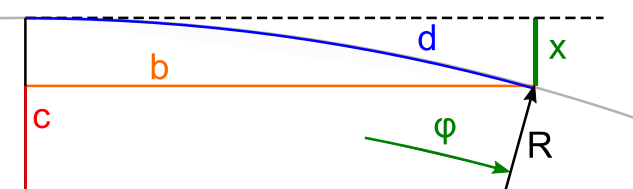
Abfallen der Oberfläche

Das Dreieck c, b, R ist ein rechtwinkliges Dreieck. Wir können c mithilfe von Trigonometrie berechnen:

(1)	$c = R \cdot \cos( \varphi )$

Aus der Distanz d lässt sich der Winkel φ berechnen:

(2)	$\varphi = d / R$

Die zur horizontalen Tangente verlängerte Linie c ist auch R. x ist also die Differenz R − c:

(3)	$x = R - c = R - R \cdot \cos( \varphi ) = R \cdot \left[ 1 - \cos( \varphi ) \right] \qquad\Rightarrow$

(4)

$x = R \cdot \big[ 1 - \cos( d / R ) \big]$

genau

(5)

$x = { d^2 \over 2 \cdot R }$

gute Näherung if d ≪ R

wobei^'

$x$ ^'	=^'	^'vertikales Abfallen von der Tangente an die Oberfläche
$R$ ^'	=^'	^'Radius der Erde
$d$ ^'	=^'	^'Distanz entlang der Oberfläche

Approximation: Wir können die Taylor-Reihe der Kosinusfunktion bis zum quadratischen Term cos(φ) ≈ 1 − φ²/2 verwenden, um eine Approximation für kleine Winkel zu erhalten:

(6)	$x = R \cdot \left[ 1 - \mathrm{cos}( d / R ) \right] \approx R \cdot \left[ 1 - \left( 1 - { (d/R)^2 \over 2 } \right) \right] = R \cdot { d^2 \over 2 \cdot R^2 } = { d^2 \over 2 \cdot R }$

Wenn wir Meilen für d und 8 Zoll/Meilen² für 1/2R verwenden, erhalten wir die berühmte Näherungsformel "8 Zoll pro Quadratmeilen" (8 inches per miles squared).

Abfallen des Horizontes von Augenhöhe

Der Abfall x ist h + c. Die blaue strichlierte Linie ist eine Symmetrielinie. Wir können also auch die Höhe h auf der rechten Seite finden, indem wir die Hypotenuse eines rechtwinkligen Dreiecks mit Winkel φ bilden. Mit Trigonometrie finden wir c = h · cos(φ). Also haben wir:

(7)	$x = h + c = h + h \cdot \cos( \varphi )$

Wir haben noch ein weiteres rechtwinkliges Dreieck mit dem Winkel φ: R+h, b, R. In diesem Dreieck ist R = (R+h) · cos(φ). Wir können also nach (/$cos(φ)/ auflösen:

(8)	$\cos( \varphi ) = { R \over R + h }$

und den Kosinus von (7) ersetzen:

(9)	$x = h + h \cdot \cos( \varphi ) = h + h \cdot { R \over R + h } \qquad \Rightarrow$

(10)

$x = h + { h \cdot R \over R + h }$

genau

(11)

$x = 2 \cdot h$

gute Näherung wenn h ≪ R

wobei^'

$x$ ^'	=^'	^'Abfall des Horizontes von Augenhöhe
$h$ ^'	=^'	^'Augenhöhe des Beobachters
$R$ ^'	=^'	^'Radius der Erde

Approximation: wenn h ≪ R können wir die Approximation R + h ≈ R anwenden:

(12)	$x = h + { h \cdot R \over R + h } \approx h + { h \cdot R \over R } = 2 \cdot h$

Abfall-Winkel des Horizontes von Augenhöhe

Den Fallwinkel φ finden wir auch an der nicht sichtbaren Ecke des rechtwinkligen Dreiecks R+h, b, R. Der Kosinus dieses Dreiecks ist:

(13)	$\cos(\varphi) = { R \over R + h }$

Auflösen nach φ ergibt:

(14)

$\varphi = \mathrm{acos} \left( { R \over R + h } \right)$

genau

(15)

$\varphi = \sqrt{ { 2 \cdot h \over R } }$

gute Näherung wenn h ≪ R

wobei^'

$\varphi$ ^'	=^'	^'Fallwinkel von Augenhöhe im Bogenmass (Radiant)
$h$ ^'	=^'	^'Augenhöhe des Beobachters
$R$ ^'	=^'	^'Radius der Erde

Approximation: Der Winkel φ kann auch durch eine asin-Funktion ausgedrückt werden, wenn wir die dritte Seite b des Dreiecks verwenden, welche ist b = √ (R + h)² − R². Das heisst φ = asin( b / (R+h) ). Die asin-Funktion kann angenähert werden zu asin(φ) ≈ φ für kleine Winkel φ, und R + h ≈ R für h ≪ R, sodass wir mehrere Vereinfachungen vornehmen können, ohne viel Genauigkeit zu verlieren:

(16)	$\varphi = \mathrm{asin} \left( { \sqrt{ (R + h)^2 - R^2 } \over R + h } \right) = \mathrm{asin} \left( { \sqrt{ h \cdot (2R + h) } \over R + h } \right) \approx \mathrm{asin} \left( \sqrt{ { 2 \cdot h \cdot R \over R^2 } } \right) = \mathrm{asin}\left( \sqrt{ { 2 \cdot h \over R } } \right)$
(17)	$\varphi \approx \sqrt{ { 2 \cdot h \over R } }$

Abfallen eines Objektes von Augenhöhe

Der Winkel φ = d/R ist einer der Winkel des rechtwinkligen Dreiecks R+h_O, R+h_T+x, b. Der Kosinus dieses Winkels ist das benachbarte R+h_O geteilt durch die Hypotenuse R+h_T+x:

(18)	$\cos(\varphi) = { R + h_\mathrm{O} \over R + h_\mathrm{T} + x }$

Wir können nach dem Nenner auflösen, der unsere Unbekannte x enthält:

(19)	$x + R + h_\mathrm{T} = { R + h_\mathrm{O} \over \cos(\varphi) } = { R + h_\mathrm{O} \over \cos(d/R) }$

Und auflösen nach x ergibt:

(20)

$x = { R + h_\mathrm{O} \over \mathrm{cos}( d / R ) } - R - h_\mathrm{T}$

wobei^'

$x$ ^'	=^'	^'Abfallen des Objektes von Augenhöhe, negativ bei Objekten oberhalb Augenhöhe
$d$ ^'	=^'	^'Entfernung zum Objekt entlang der Oberfläche (Sichtlinie oder entlang der Oberfläche ist ungefähr gleich)
$h_\mathrm{O}$ ^'	=^'	^'Augenhöhe des Beobachters
$h_\mathrm{T}$ ^'	=^'	^'Höhe des Objektes
$R$ ^'	=^'	^'Radius der Erde

Beachte, für kleine Winkel φ, d.h. wenn h_O ≪ R und h_T ≪ R, dann ist y ≈ x. y ist die Ankathete eines ähnlichen rechtwinkligen Dreiecks mit der Hypotenuse x. Wir können also den genauen Wert für y erhalten, indem wir (20) mit (/$cos(d/R)/ multiplizieren):

(21)

$y = R + h_\mathrm{O} - ( R + h_\mathrm{T} ) \cdot \mathrm{cos}( d / R )$

wobei^'

$y$ ^'	=^'	^'Abfallen des Objektes von Augenhöhe, negativ bei Objekten oberhalb Augenhöhe
$d$ ^'	=^'	^'Entfernung zum Objekt entlang der Oberfläche (Sichtlinie oder entlang der Oberfläche ist ungefähr gleich)
$h_\mathrm{O}$ ^'	=^'	^'Augenhöhe des Beobachters
$h_\mathrm{T}$ ^'	=^'	^'Höhe des Objektes
$R$ ^'	=^'	^'Radius der Erde

Winkelgrösse

(22)

$\theta = 2 \cdot \mathrm{atan} \left( { s \over 2 \cdot d } \right)$

genau

(23)

$\theta = { s \over d } \qquad\Leftrightarrow\qquad s = \theta \cdot d$

gute Näherung wenn s ≪ d

wobei^'

$\theta$ ^'	=^'	^'Winkelgrösse in Bogenmass (Radiant)
$s$ ^'	=^'	^'Grösse des Objekts, gemessen senkrecht zur Sichtlinie
$d$ ^'	=^'	^'Entfernung entlang der Sichtlinie

Approximation: Für kleine Winkel φ können wir approximieren atan(φ) ≈ φ. Der Winkel φ ist klein, wenn s ≪ d. In diesem Fall erhalten wir:

(24)	$\theta = 2 \cdot \mathrm{atan} \left( { s \over 2 \cdot d } \right) \approx 2 \cdot \left( { s \over 2 \cdot d } \right) = { s \over d }$

Refraktions-Winkel und Anhebung

Die magenta Linie ist die direkte Sichtlinie des Beobachters zu einem Ziel. Der orangefarbene Bogen ist der entsprechende gebogene Lichtstrahl mit Krümmungsradius r. Der Refraktionswinkel ist ρ.

Wir haben ein rechtwinkliges Dreieck r, d/2, b mit einem Winkel ρ. Wir können Trigonometrie anwenden, um den Sinus von ρ zu berechnen:

(25)	$\sin(\rho) = { d/2 \over r }$

Die Krümmung 1/r des Lichtstrahls ist definiert durch den Refraktions-Koeffizienten:

(26)	$k = { 1 \over r } \cdot R \qquad\Rightarrow\qquad { 1 \over r } = { k \over R }$

Wir erhalten also:

(27)	$\sin(\rho) = { 1 \over r } \cdot { d \over 2 } = { k \over R } \cdot { d \over 2 }$

Für kleine Winkel ρ, d.h. wenn d ≪ R, können wir sin(ρ) ≈ ρ approximieren und unter Anwendung der Gleichung für Winkelgrösse können wir die scheinbare Anhebung l aufgrund der Refraktion berechnen:

(28)

$\rho = { k \over R } \cdot { d \over 2 }$

(29)

$l = \rho \cdot d = { k \over R } \cdot { d^2 \over 2 }$

wobei^'

$\rho$ ^'	=^'	^'Refraktions-Winkel
$l$ ^'	=^'	^'scheinbare Anhebung des Ziels aufgrund der Refraktion in Bezug auf eine feste Bezugslinie wie Augenhöhe des Betrachters
$k$ ^'	=^'	^'Refraktions-Koeffizient
$k/R$ ^'	=^'	^'1/r = Krümmung des Lichtstrahls
$r$ ^'	=^'	^'Krümmungs-Radius des Lichtstrahls
$d$ ^'	=^'	^'Distanz vom Beobachter zum Ziel entlang der Oberfläche
$R$ ^'	=^'	^'Radius der Erde

Sichtlinien-Distanz zum Horizont

Wir können Pythagoras auf das rechtwinklige Dreieck R+h, d, R anwenden, um unsere Unbekannte zu erhalten:

(30)

$d = \sqrt{ (R + h)^2 - R^2 }$

genau

(31)

$d = \sqrt{ 2 \cdot R \cdot h }$

gute Näherung wenn h ≪ R

wobei^'

$d$ ^'	=^'	^'Sichtlinien-Distanz vom Auge des Beobachters zum Horizont
$h$ ^'	=^'	^'Augenhöhe des Beobachters
$R$ ^'	=^'	^'Radius der Erde

Approximation: Wir können approximieren (R+h)² − R² ≈ 2·R·h falls h ≪ R:

(32)	$d = \sqrt{ (R + h)^2 - R^2 } = \sqrt{ R^2 + 2 \cdot R \cdot h + h^2 - R^2 } = \sqrt{ 2 \cdot R \cdot h + h^2 } \approx \sqrt{ 2 \cdot R \cdot h }$

Der Ausdruck 2·R·h ist viel grösser als h² wenn h ≪ R. Also können wir h² vernachlässigen.

About	Walter Bislin (wabis)
Rights	Public Domain

More	Page Infos / Sitemap
Created	Dienstag, 28. Dezember 2021

Scroll to	Top of Page
Changed	Mittwoch, 12. Januar 2022

WaBis

walter.bislins.ch

Walter Bislin's Blog-De

Rainy Lake Experiment: Formeln

Terrestrial Refraktion

Radius of the Earth

Koordinaten-Transformationen

Abfallen der Oberfläche

Abfallen des Horizontes von Augenhöhe

Abfall-Winkel des Horizontes von Augenhöhe

Abfallen eines Objektes von Augenhöhe

Winkelgrösse

Refraktions-Winkel und Anhebung

Sichtlinien-Distanz zum Horizont

Blog-Funktionen

Pages

Auf dieser Seite