Im Gegensatz zu Triebwerk-Simulationsprogrammen, welche alle internen Parameter berechnen, brauche ich nur ein vereinfachtes Modell, welches mir den Zusammenhang zwischen N₁, Geschwindigkeit des Flugzeugs und resultierendem Schub liefert und das Ganze nur für Standardatmosphäre auf Meereshöhe. Interne Parameter werden nicht simuliert sondern durch Formeln approximiert, soweit die Parameter für die Berechnung des Schubes benötigt werden.

Formel für die Schubkraft

Querschnitt durch ein zweiachsiges Turbofan-Triebwerk

Die totale Schubkraft F (Netto Schubkraft) eines Triebwerks ist abhängig von internen Faktoren wie der Verteilung des Luftmassenflusses ${\dot m}_0$ im Triebwerk, der Geschwindigkeiten v_i dieser Luftströmungen und externen Faktoren wie der Geschwindigkeit v₀ des Flugzeugs und Eigenschaften der Luft wie Druck, Temperatur und Luftdichte.

Die Schubkraft F_i ist das Produkt von Luftmassenstrom ${\dot m}_i$ (Luftmasse, die in einer bestimmten Zeit ausgestossen wird) und der Geschwindigkeit v_i der enstprechenden Luftmasse:

Durch den inneren Aufbau eines Triebwerks ergibt sich daraus die folgende allgemeine Formel für den Schub eines Turbofan-Triebwerks [1]:

Für ein vereinfachtes Modell können folgende Annahmen und Vereinfachungen getroffen werden:

• Der Druck p₁ in der primären Schubdüse entspricht dem Umgebungsdruck: p₁ = p₀.
• Die Massenstromanteile von Brennstoff ${\dot m}_\mathrm{B}$ und Zapfluft ${\dot m}_\mathrm{Z}$ werden vernachlässigt.

Damit vereinfacht sich die Schub-Formel (2) zu:

Einfluss von Geschwindigkeit, Luftdichte und Temperatur auf den Schub

Einfluss von Geschwindigkeit und Staudruck auf den Schub eines Triebwerks [2]

Die obige Formel (3) gilt nur angenähert für Standardatmosphäre und Geschwindigkeiten unter Mach 0,3. Die Massenflüsse und Strömungsgeschwindigkeiten durch das Triebwerk hängen auch von äusseren Einflüssen wie Geschwindigkeit des Flugzeugs, Luftdichte und Temperatur ab. Luftdichte und Temperatur hängen von Wetterbedingung und Flughöhe ab. Fliegt das Flugzeug schnell genug (mehr als Mach 0,3), so macht sich die Kompressibilität der Luft bemerkbar, indem die Luftdichte und Temperatur erhöht werden, je schneller das Flugzeug fliegt.

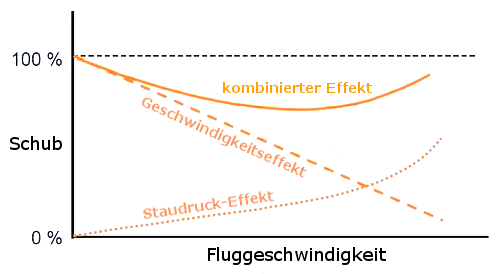
Schub als Funktion von Geschwindigkeit für verschiedene Bypass-Werte [3]

Die Einflüsse wirken wiefolgt:

Je höher das Flugzeug fliegt, umso niedriger werden Luftdichte und Temperatur, bis zu einer Höhe von 11 km. Zwischen 11 km und 20 km Höhe bleibt die Temperatur konstant, wogegen die Luftdichte weiter abnimmt. Für Berechnungen von Druck, Luftdichte und Temperatur in bestimmten Höhen siehe Schichtenmodell (Barometrische Höhenformel).

Der Brutto-Schub des Triebwerks nimmt proportional mit der Luftdichte ab. Niedrigere Temperturen erhöhen die Leistung leicht. Der Brutto-Schub nimmt unter diesen Einflüssen insgesamt mit der Flughöhe erheblich ab (ca. 55% Schub bei 11 km Höhe).

Wenn ein Flugzeug schnell fliegt, staut sich die Luftmasse vor dem Flugzeug. Man spricht vom Staudruck (dynamic pressure). Dieser erhöht die lokale Luftdichte und Temperatur vor dem Flugzeug umso mehr, je näher sich die Fluggeschwindigkeit der Schallgeschwindigkeit nähert. Diese Erhöhung der Luftdichte aufgrund des Staudrucks erhöht die Leistung der Gasturbine. Bei einem reinen Turbojet Triebwerk (Triebwerk ohne Bypass, also ohne Fan) wird die Leistung soweit gesteigert, dass der Verlust aufgrund der Geschwindigkeitsdifferenz von Flugzeug und Abgasstrahl (Formel (3)) kompensiert wird. Bei einem Turbojet Triebwerk wird daher gesagt, der Schub hänge praktisch nicht von der Fluggeschwindigkeit ab.

Bei einem Turbofan-Triebwerk mit seinem grossen Bypass-Verhältnis trägt die Gasturbine, also das Kerntriebwerk, nur einen Bruchteil zum Schub bei. Nur das Kerntriebwerkt erhöht seine Leistung aufgrund des Staudrucks erheblich. Der Fan steigert seine Leistung mit der Geschwindigkeit nur in dem Verhältnis, wie es der Zunahme der Luftdichte aufgrund der Geschwindigkeit (Zunahme des Staudrucks) entspricht. Daher nimmt der kombinierte Netto-Schub von Kerntiebwerk und Fan im Vergleich zu einem reinen Turbojet Triebwerk mit der Geschwindigkeit trotzdem ab, wenn auch nicht so stark wie ohne Berücksichtigung des Staudrucks. Je grösser das Bypass Verhältnis, umso grösser die Abnahme. Die Abnahme des Nettoschubs liegt bei einem Turbofan-Triebwerk irgendwo zwischen dem mit der Formel (3) berechneten Wert und dem entsprechenden Standschub, siehe Bild. [3]

Da ich in dieser Arbeit nur ein Triebwerks-Modell für Geschwindigkeiten unter 200 kt benötige, kann ich obige Einflüsse vernachlässigen.

Formel für den Gegenschub

Schnittbild Triebwerk im Umkehrschub-Betrieb

Wenn Gegenschub gegeben wird (Reverse Thrust), wird der Fan-Massenstrom ${\dot m}_2$ in einem bestimmten Winkel θ seitwärts nach vorne abgelenkt (siehe Bild).

Der Massenstrom ${\dot m}_1$ des Kerntriebwerks wird weiterhin nach hinten ausgestossen und erzeugt den Schubanteil F₁.

Der vom Fan-Massenstrom erzeugte Schubanteil F₂ wirkt nur teilweise nach vorne als Gegenschub. Der als Gegenschub anrechenbare Anteil F_2,x beträgt:

Da cos(θ) = 0,5 ist, wirkt nur die halbe vom Fan erzeugte Schubkraft als Gegenschub. Der vom Kerntriebwerk erzeugte Schub F₁ wirkt weiterhin nach hinten und schwächt dadurch den Gegenschub. Tatsächlich resultiert nur dann ein bremsender Netto-Schub, wenn F_2,x grösser als F₁ ist.

Die Formel für den Gegenschub lautet:

Das CFM56-5A3 Triebwerk

Als Modell-Beispiel verwende ich die Daten des CFM56-5A3 Turbofan-Triebwerkes, welches zum Beispiel bei einem Airbus A320 zum Einsatz kommt. Das CFM56-5A3 ist ein zweiachsiges Turbofan-Triebwerk mit nicht gemischtem Fluss (unmixed flow turbofan).

Technische Daten des CFM56-5A3 [4]

Obige Angaben beziehen sich auf den maximalen Startschub unter Standardatmosphäre (Temperatur = 15 °C, Luftdruck = 1013,25 hPa) und Stillstand des Flugzeugs (v₀ = 0).

Mass flow ist definiert als: ${\dot m}_0 = {\dot m}_1 + {\dot m}_2$.

Bypass ratio ist definiert als: $\mu = {\dot m}_2 / {\dot m}_1$.

Die Bypass ratio ist keine Konstante sondern verändert sich in Abhängigkeit der verschiedenen Betriebsparameter.

Das Triebwerks-Modell

Für die Schubberechnung benötige ich die einzelnen Massenflüsse ${\dot m}_i$ und Strömungsgeschwindigkeiten v_i in Abhängigkeit der relativen Drehzahl N₁ des Fan. Die relative Drehzahl des Fan wird im Cockpit in Prozent N₁ der Auslegungsdrehzahl des Triebwerks angezeigt.

Aus dem Datenblatt eines Triebwerkes kann ich den maximalen Schub F_max, den maximalen totalen Massenfluss ${\dot m}_{0,\mathrm{max}}$ und das Aufteilungsverhältnis μ dieses Flussen in ${\dot m}_{1,\mathrm{max}}$ und ${\dot m}_{2,\mathrm{max}}$ herauslesen.

Mit diesen Daten alleine kann kein Triebwerks-Modell berechnet werden. Weitere Informationen über Turbofan-Triebwerke müssen gefunden werden.

Ich benötige noch folgende Zusammenhänge:

Obige Zusammenhänge fasse ich zusammen in einem Modell des Triebwerks und spiele in einer Simulation damit:

Quellen

[1]

Flugzeugtriebwerke: Grundlagen, Aero-Thermodynamik, Kreisprozesse; von Willy J. G. Bräunling; Beispiel 5-5; Seite 243
http://books.google.ch/books?id=2yrCF9-XE7YC&pg=PA269&lpg=PA269&dq=triebwerk+n1&source=bl&ots=4Gc9Iavrki&sig=qGM8daUbiLh20TzOZphjc4AXw-M&hl=de&sa=X&ei=WN1xT9vPMsHNhAeb4OynAQ&ved=0CCQQ6AEwADgK#v=onepage&q=triebwerk%20n1&f=false

[2]

www.smartcockpit.com; Jet Engine Basics - SmartCockpit
http://www.smartcockpit.com/docs/Jet_Engines_Basics.pdf

[3][a][b]

adg.stanford.edu; Thrust Variation with Speed and Altitude
http://adg.stanford.edu/aa241/propulsion/tvshv.html

[4]

CFM Technical Data
http://www.cfm56.com/products/cfm-technical-data