WaBis
walter.bislins.ch
Comparison of Globe and Flat-Earth Model Predictions with Reality
All Globe and Flat-Earth Model Predictions are computed with my Curvature App. Please note that the horizon of the Flat-Earth Model always is at Eye-Level of the Globe Model. On the Globe the horizon is never at Eye-Level so all objects near or behind the horizon are below Eye-Level too.
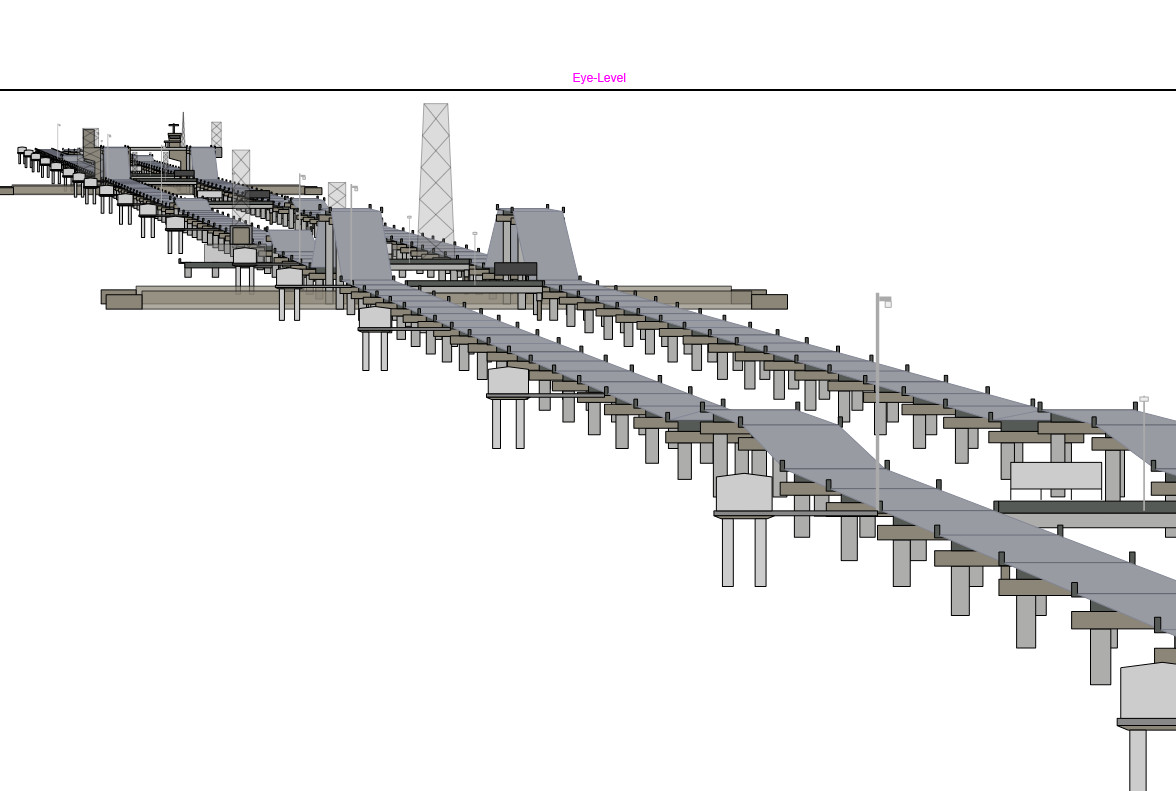
Causeway View from Marriott Hotel
- Swap
- Globe Model
- Flat-Earth Model
This scene shows the 38 km long Causeway Bridge at Lake Pontchartrain, Lousiana. The image was taken from the 15th floor of the Marriott Hotel at the south side of the lake using a telescope with a zoom factor of about 2000 mm (35 mm equivalent).
Source: Screenshot from Soundly's Youtube Channel
Note: please click the description below the image to open the Curvature App and load the corresponding simulation.
Causeway GNSS Data match the Globe Model perfectly
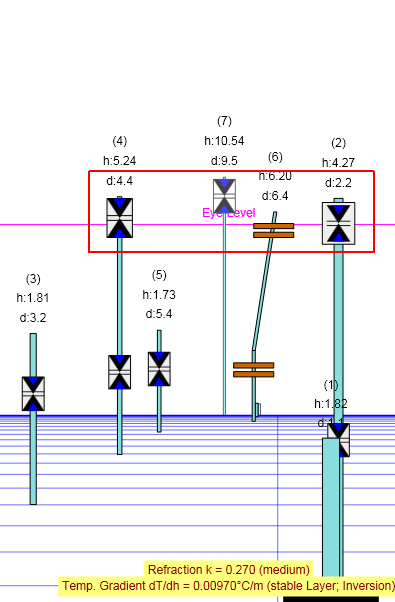
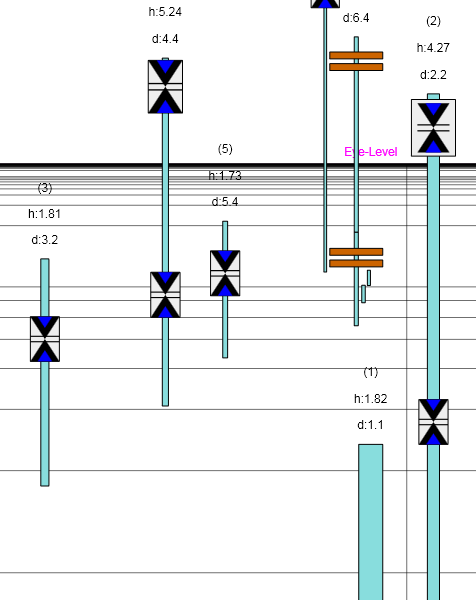
Jesse Kozlowski measured both lanes of the Causeway using Differential GPS to 5 cm accuracy. The data gathered are 3D cartesian coordines, which represent points in space. The GPS measurements are not affected by refraction or perspective. So they represent the real geometric positions in space.
I imported the data in my Geo-Data Visualisation and Calculator App and superimposed an image from Soundly, taken from the 15th floor of the Marriott Hotel. Jesse also measured the 3D location of the window, from where the image was taken. So I could position the virtual camera of my App at this 3D position and align the image and the data as shown in the images on the right.
On this image refraction was less than on the image on the right. The image matches very well with the raw geometry data of the GPS/GNSS measurements.
On this image refraction was stronger than on the left image. It loomes the far end of the bridge and the water tower recognizable up.
The same GPS/GNSS data matches the 3D Globe Model of the Causeway with refraction set to zero perfectly (click on the image to zoom in).
It is difficult to see the alignment of the data with the 3D Globe Model of the Causeway at the far end. So I displaced the measurements to the left and algined them with the base of the huts. Now we can recognize, that the measurements and the 3D model match perfectly.
Whith GPS/GNSS technology we have a method to measure the real geometry of the Causeway bridge. The geometry of the bridge is curving over the horizon, which means water is curved. The measured geometry matches the Globe Model of the bridge perfectly as expected, because the Globe Model is based on a sphere with radius 6371 km and the data gathered confirms that the earth is a spheere with radius 6371 km, see Causeway Measuring Radius of the Earth. The images show only slight deviations from the geometry due to refraction but the overall appearance is the same. So the images show definitively the real curvature of the earth.
The geometric horizon is where the datapoints begin to curve down (lighter brownish color of the points). The apparent horizon appears farther away and higher due to refraction (looming).
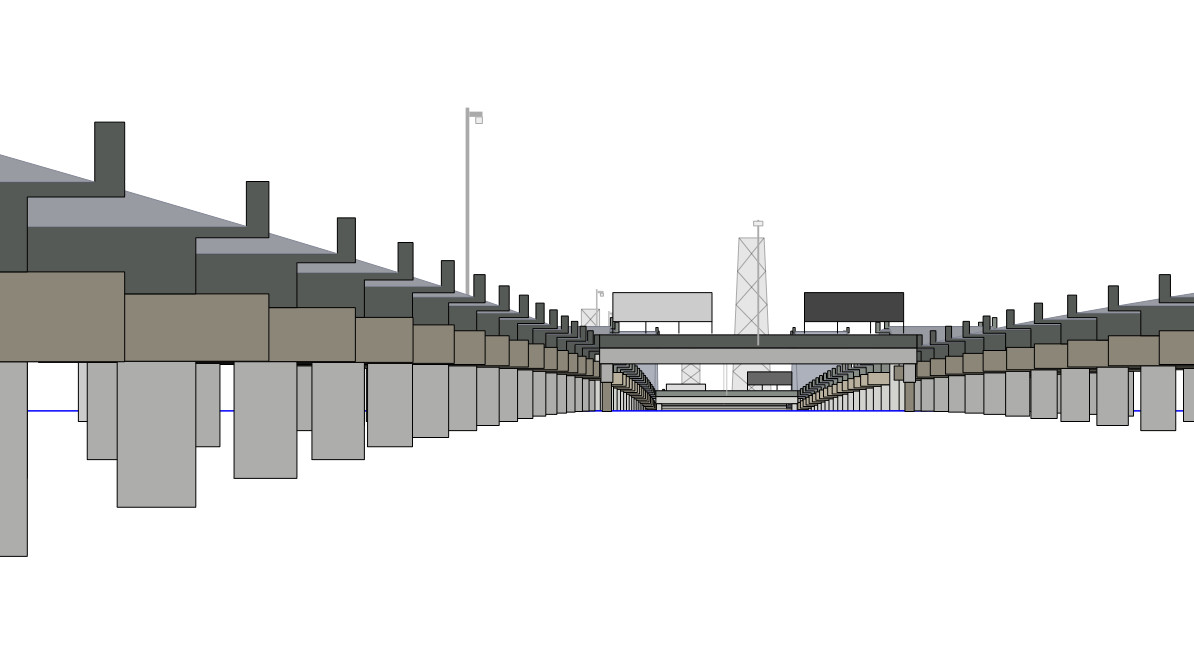
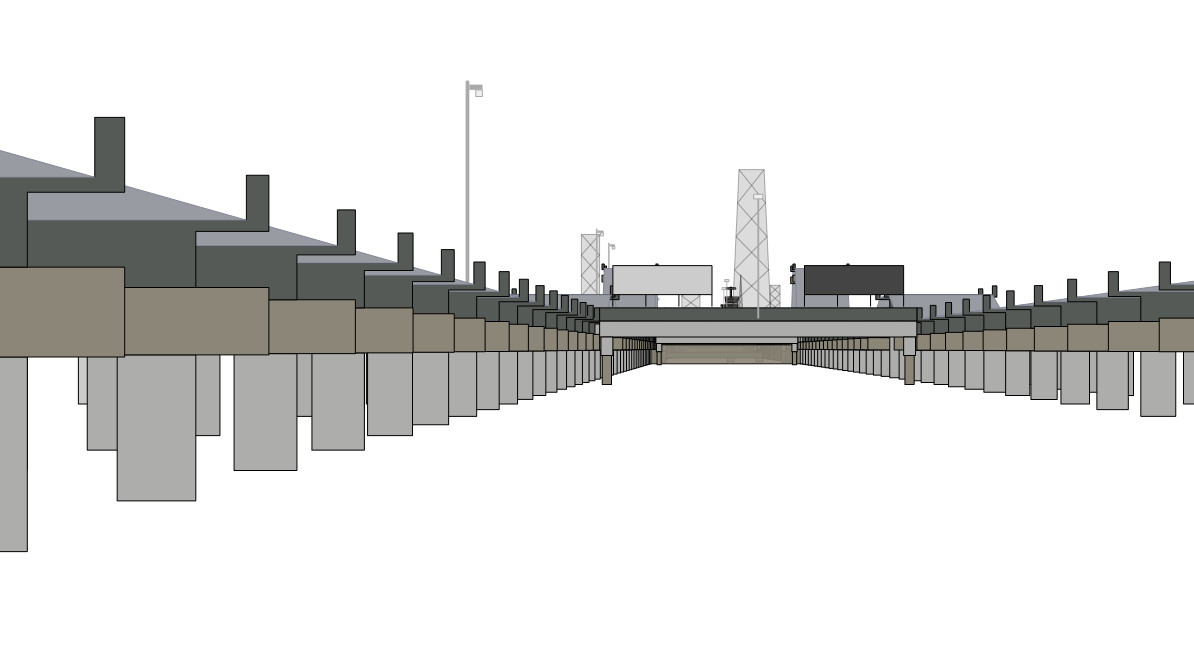
Causeway View to Hotel Marriott
- Swap
- Globe Model
- Flat-Earth Model
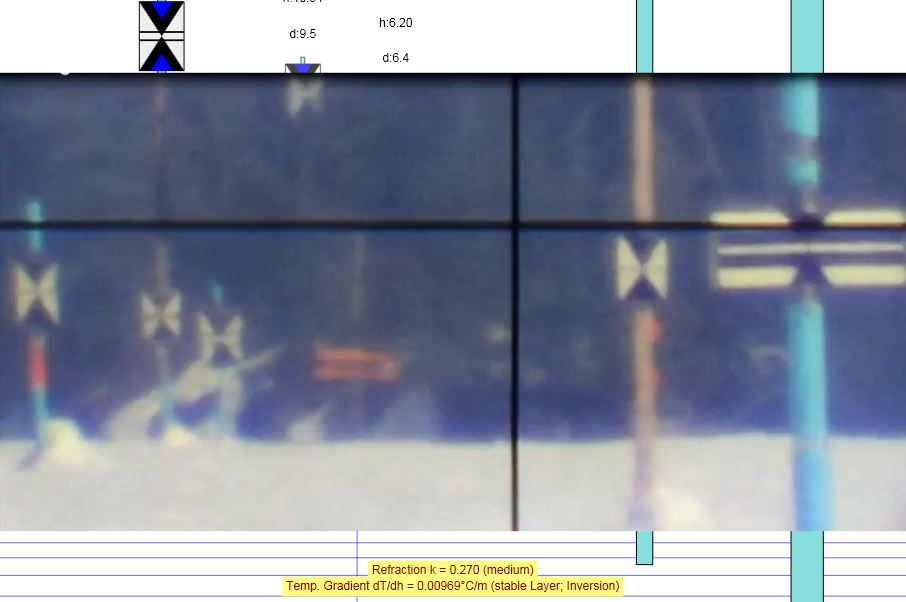
This scene shows the 38 km long Causeway Bridge at Lake Pontchartrain from the north side looking to the Marriott Hotel (Zoom about 3000 mm). Note that in the Theodolite View the horizontal line of the crosshair of the Theodolite is exactly at Eye-Level.
- Screenshot from: Blink Test Marriott (Flat Earth Debunk) by Soundly
- Theodolite View: Lake Pontchartrain 12/10/17 - Marriott Hotel Viewed From North Shore by Jesse Kozlowski
Causeway View Left
- Swap
- Globe Model
- Flat-Earth Model
Source: Screenshot from Soundly's Youtube Channel
Causeway View Center
- Swap
- Globe Model
- Flat-Earth Model
Source: Screenshot from Soundly's Youtube Channel
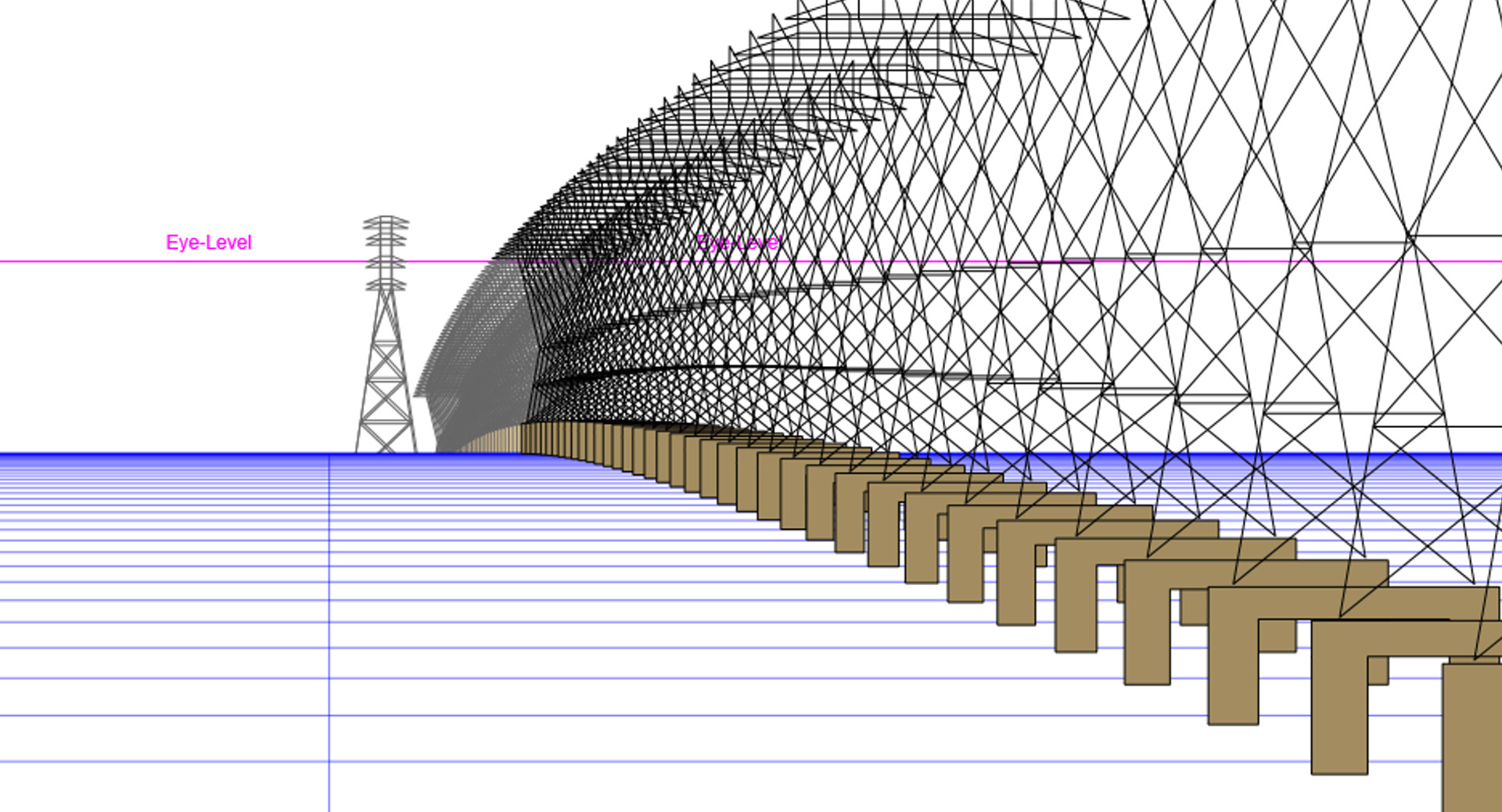
Lake Ponchartrain Transmission Line
- Swap
- Globe Model
- Flat-Earth Model
This scene shows one of the Lake Pontchartrain Transmission Lines, which crosses the lake in a perfectly straigh line. Over a distance of 25.9 km there are 85 identical towers with a separation of 300 m. The towers have a height of 23 m. The last 2 towers have a height of 64 m.
Image from: Soundly Proving the Curvature of the Earth at Lake Pontchartrain (Metabunk); Soundly's Youtube Channel
Steven Elliott has a very good Tutorial how to create a model of the transmission lines in Blender.
The Rainy Lake Experiment
The Rainy Lake Experiment was designed to show, how we can figure out the shape of the earth, Flat or a Globe, by observing a clever arrangement of targets over a distance of 10 km, taking terrestrial refraction into account and using modern equipment. The experiment is an advanced version of the Bedford Level experiment executed in 1838. The Experiment leads to the only conclusion that the earth is a Globe with a radius of 6371 km.
- Rainy Lake Experiment Animation
- The Rainy Lake Experiment, full report
- Swap
- Globe Prediction
- Flat Earth Prediction
 The Flat Earth model predicts that all Bedford targets appear aligned with the horizon and eye level, which does not match the observation. ⇒more
The Flat Earth model predicts that all Bedford targets appear aligned with the horizon and eye level, which does not match the observation. ⇒more
 The Computer Model shows the predicted image using the measured target center heights, which match the observations very well. The Flat Earth prediction does not match the observation at all. ⇒more
The Computer Model shows the predicted image using the measured target center heights, which match the observations very well. The Flat Earth prediction does not match the observation at all. ⇒more
Below Eye Level, Miles Davis
- Swap
- Globe Model
- Flat-Earth Model
- Blink Test
- Reality
- Globe Model Overlayed
- Globe Model
This observation from Miles Davis, like all other observations on this page, confirms without any doubt that the earth is a Globe. Miles Davis is at an altidude of 210 m. The middle bridge tower is at sea level and has a height of 210 m. All hills in the distance are far taller than 210 m but they appear below the 210 m line or only very slightly above.
Note that the bridge towers and hills are all far below eye level. This can only be recognized in reality by using an auto level or theodolite. But anyway, the Flat Earth Model Prediction looks nowhere near like the image, while the Globe Model Prediction, using Standard Refraction, matches perfectly!
Note also, that even the bridge towers are the same height as the observer, they apear below eye level, because the earth curves down with increasing distance.
Observation Data Miles Davis
- Observer location: Traprain Law 55°57'47.32"N 2°40'21.19"W
- Bridge location: Edinburgh 56°0'16.38"N 3°24'45.32"W
You can click the links in the table below to open my Curvature App with the corresponding hill shown. You can than play with the settings. To change the transparency of the overlayed image, click on the image. Clicking left of the center makes it more transparent, clicking right more opaque.
| Hill | Height | Distance | SidePos | Coordinates |
|---|---|---|---|---|
| Earl's Seat | 578 m | 101.6 km | −3000 m | 56°1'31.35"N 4°17'49.79"W |
| Dun Brach | 540 m | 97.2 km | −2700 m | 56°1'37.89"N 4°13'16.05"W |
| Meikle Bin | 570 m | 91.8 km | −3150 m | 56°0'50.40"N 4°8'18.11"W |
| Cairnoch Hill | 413 m | 89.1 km | 450 m | 56°1'14.56"N 4°0'2.16"W |
| Stronend | 511 m | 96.4 km | 3460 m | 56°4'43.46"N 4°12'10.34"W |
SidePos: is the horizontal distance from the center line of the image at the distance of the hill.
The observer Height in the Curvature App is set to 210 m and the Zoom to 420 mm. Standard Refraction of k = 0.17 is set. The measuring rods (bridge towers) are at a distance of 46.5 km from the observer and have a size of 210 m. Data providet by Miles Davis and confirmed by me using google earth.
Confirmation of Drop from Auto Level
As the Curvature App image on the left above indicates with the magenta eye level line, the top of the bigger tower in Miles images has to be below eye level due to the curvature of the earth. Miles did not use an auto level so we can not say how much drop there is. But a Youtube user called Creamy Pasta did exactly the same observation at another day using an auto level (image on the right).
- Traprain Law visit by Creamy Pasta on Youtube
The 2 short lines on the vertical crosshair mark 5 mrad (milli rad) angle. The horizontal line marks eye level of the observer, which was at 210 m altitude. From that we can measure the drop angle α to the top of the tower by counting pixels in a graphics program. I measured a drop angle of 3.16 mrad = 0.181°.
How much drop angle does the globe predict? Matching the image with my Curvature App I got a refraction prevealing at the time the image was taken of k = 0.135, which is Standard Refraction.
Now lets calculate the expected drop angle of the top of the tower for the globe model and see if it matches the measured drop angle of 0.181°.
The drop angle φ due to the curvature of the earth, without refraction, can be calculated as follows:
| (1) | |||||||||||||
| where' |
|
Standard refraction loomes objects up. So we see a slightly smaller drop angle than the curvature drop angle. The refraction angle can be calculated as follows:
| (2) | |||||||||||||
| where' |
|
So the expected drop angle according to the globe model, taking standard refraction into account, is:
| (3) |
| |||||||||
| where' |
|
This is exactly what we measure from the image through the auto level. This confirms again the earth is a globe with radius 6371 km.
Salt Lake City
Observation of Salt Lake City from 40 km distance (top 3 images parts), showing how the water horizon hides the bottom part of the city as predicded by the Globe Model. The Flat-Earth model predictions do never hide anything of the city and do not match the footage at all.
 Globe Model Prediction of Refraction Simulator
Globe Model Prediction of Refraction Simulator Flat-Earth Prediction of Refraction Simulator
Flat-Earth Prediction of Refraction Simulator- Swap
- Globe Model
- Flat-Earth Model
- Blink Test
- Reality
- Globe Model
City observed and simulated at observer heights of 0.5 m, 1.5 m and 7.5 m. The bottom image part is from another location and higher up to show that the city is about 100 m above the Salt Lake.
Note that the simulation took the bottom image as the background. Because this image is taken from a different angle and zoom than the top 3 real images, the viewing angle and zoom to the buildings in the simulations do not match the footage. But the hidden parts do match because the vertical scaling of the buildings is the same in the simulation as on the footage.
Because the refraction was not known I had to try to find a refraction curve that matches the footage. I found that the water was probably slightly warmer than the air and some Stooping was goeing on. The Simulation shows, that no matter whether you chose zero Refraction, Standard Refraction or the Refraction Curve I used, there are always some parts of the bottom of the city and the buildings hidden from 1.5 m to 7.5 m. Only the amount and the distortion changes slightly.
Please try the Refraction Simulator yourself.
Comcast Skyscraper from Apple Pie Hill
- Swap
- Globe Model
- Flat-Earth Model
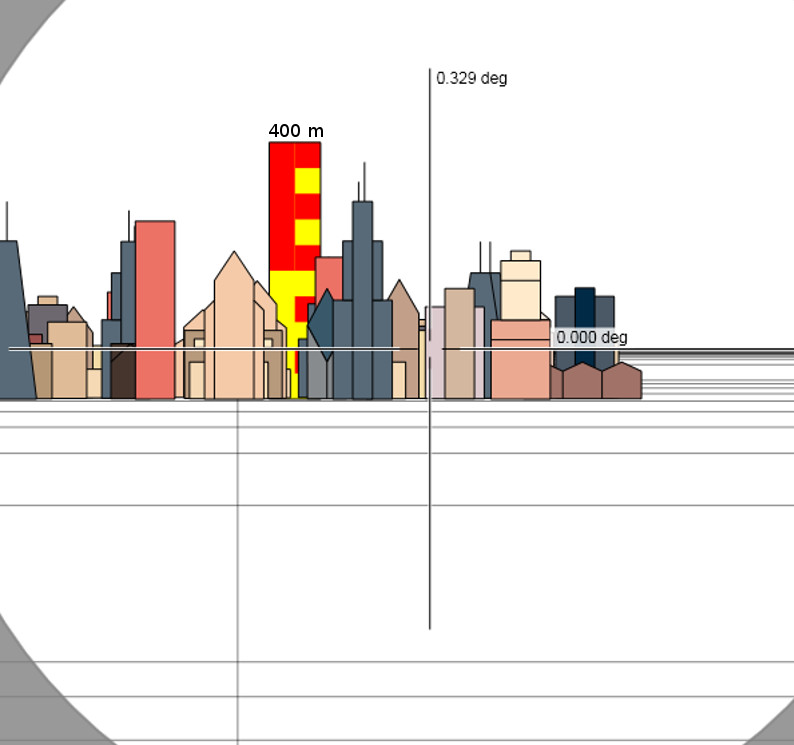
View to the Comcast Skyscraper of Philadelphia (gray building left of the crosshair) through the Auto Level of Jesse Kozlowski (a Geodetic Surveyor) from on top of Apple Pie Hill (62 m) Fire Tower (18 m) in southern New Jersey.
The Earth’s Curvature Plainly Visible, Viewing Philadelphia From Apple Pie Hill In New Jersey by Jesse Kozlowski
Detailed documentation of the observation with all data
The horizontal crosshair is at auto level elevation of about 78 m (256 Feet) NAVD88 and shows the Eye-Level plane from the observers location. The Eye-Level plane is perpendicular to the vertical at the observer location. The distance to the top southeast corner of the Comcast Center is 52.15 km (171,100.8 Feet = 32.4 Miles). The top of the skyscraper is at elevation 307.85 m (1010 Feet) NAVD88.
The crosshair (Eye-Level Plane) intersects the Comcast building at approximately 42 m (138 feet) +/- down from the top at 266 m (873 Feet). This is because the earth curves down. On a Flat Earth the crosshair (Eye-Level Plane) would intersect the building at Eye-Level altitude of 72 m, that is about 2 scales from the bottom on the measuring rod..
A Refraction Coefficient of k = 0.13 is applied on the Globe Model, which corresponds to Standard Refraction over land.
The yellow/red measuring rod in the model is 400 m tall with a 40 m scaling. The horizon on the Globe Model is at a distance of 33.8 km (21.0 Miles) and has dropped 156 m (512 Feet) from Eye-Level or 78 m (256 Feet) from sea level corresponding to a Dip Angle of 0.264° from Eye-Level.
Oil Platform Grace
- Swap
- Globe Model
- Flat-Earth Model
Distance to Oil Platform = 28 km; Height = 37.2 m; Observer Altitude = 72 m; Anacapa Island Distance = 50.1 km; Height = 75 m; Zoom = 2000 mm
You can find Some graphical Explanation for this scene and a Demo in the Curvature App with all data to the scene. See also Video Oil Platforms and Islands | Observation and Analysis from Jon McIntyre
No amount of refraction can produce this image on a flat earth!
Windfarm Ormonde

 Panorama Image from Video footage of Miles Davis Flat-Earth: Earth Shape Tourists UK, St Bees Episode 1
Panorama Image from Video footage of Miles Davis Flat-Earth: Earth Shape Tourists UK, St Bees Episode 1- Blink Test
- Reality
- Globe Model Overlay
- Globe Model
- Flat-Earth Model
View from St. Bees (GB) to Ormonde Windfarm:
Distance = 43.6 km; Observer Altitude = 14 m; Refraction = 0.2 (medium); Hub Height = 88 m; Tides = 2 m; Hidden = 57..75 m
Images from the ISS

 Test whether the graphics of the simulation matches a real image taken from the ISS:
Test whether the graphics of the simulation matches a real image taken from the ISS:Height = 400 km; 35mm focal lengt f = 28 mm; Line Spacing 48.91 km
Date of recording: 16.09.2016 20:55; Source: NASA; Original image with EXIF Informations

 Test whether the graphics of the simulation matches a real image taken from the ISS:
Test whether the graphics of the simulation matches a real image taken from the ISS:Height = 400 km; 35mm focal lengt f = 28 mm; Line Spacing 48.91 km
Date of recording: 16.09.2016 20:55; Source: NASA; Original image with EXIF Informations
- Blink Test
- Reality
- Globe Model Overlay
This image was taken by one of the astronauts Sergey Ryzhikov, Shane Kimbrough, Andrey Borisenko, Kate Rubins, Commander Anatoly Ivanishin or Takuya Onishi on board of the ISS Expedition 49 using a NIKON D4 camera using a 28 mm wide angle lens (35 mm equivalent, no fisheye). Links to the original image and all EXIF data are provided.

 Another picture taken from the ISS showing penumbra from the solar eclipse.
Another picture taken from the ISS showing penumbra from the solar eclipse.Height = 400 km; 35mm focal length f = 20 mm; Line Spacing 55.6 km
Original image with EXIF Informations

 Another picture taken from the ISS showing penumbra from the solar eclipse.
Another picture taken from the ISS showing penumbra from the solar eclipse.Height = 400 km; 35mm focal length f = 20 mm; Line Spacing 55.6 km
Original image with EXIF Informations
- Blink Test
- Reality
- Globe Model Overlay
This image shows the moon's shadow (penumbra) from the solar eclipse on Aug. 21, 2017. It was taken by one of the astronauts Randy Bresnik, Jack Fischer, Peggy Whitson, Paolo Nespoli, Commander Fyodor Yurchikhin or Sergey Ryazanskiy using a NIKON D4 camera using a 20 mm wide angle lens (35 mm equivalent, no fisheye). Links to the original image and all EXIF data are provided.
Elon Musk's Tesla in Space
- Blink Test
- Reality
- Globe Model Overlay
- Blink Test
- Reality
- Globe Model Overlay
Comments
Heyo, der absolute Hammer!
Flat Earth rest in peace!
Vielen Dank!
Gruess
Marc
why on flat earth skyline starts from eye level?? wtf with u? and where is perspective, dude?
Skyline on FE starts from eye level if your eyes are near the ground. As higher you go, the lower the skyline appears with respect to the horizon line, depending on the distance to the skyline. Check out Finding the curvature of the Earth.
Perspective is built into the model. In fact the model is based on perspective. Perspective says, the angular size of objects decreases with distance, so they appear smaller. But you can zoom in to magnify the object to any size, depending on the zoom capabilities of your device.
Walter, you have impressed me in every way imaginable with your flawless work! Keep posting evidence for the globe! Because the globe, is reality, and the space pizza, is a fantasy.
Feine Arbeit! Hochgradig beindruckend, alles unter einen Hut zu bringen. Ich habe schon Probleme mit Google die notwendigen Formeln und Modelle zu finden, und das hier ist alles in einer Packung!
Hahaha its so funny watching you match up the curve of the earth on the ISS when they confirm they use GoPro FishEye lenses, and the fact that the ISS only see's 3% of the earth at any one time, it should show a flat horizon silly.. You have literally just matched a GoPro fisheye to the curve of the earth hahahah:
https://www.sciencealert.com/
ISS astronauts do not use Fisheye lenses for Images of the Earth
Gleem: they confirm they use GoPro FishEye lenses
Do you really think NASA and all astronauts use all the same camera for all images they ever take? Only because some of the images may be taken with a GoPro camera does not mean that ALL images are taken with a GoPro camera, agreed?
The linked article refers to a camera used at space walks, which have to record as much of the field of view as possible for documentation and review. For such applications it is common (on earth too) to use GoPro cameras with fisheye lenses. But the images of the earth are taken by full frame cameras with expensive non distorting lenses.
NASA states on each image they publish what camera and lenses are used. This infos are embeded in the original images and I listed the relevant data below the images. I have chosen deliberately images that were not taken using fisheye lenses, because my App can not simulate fisheye lenses. You can go to the linked website, download the original full size image and see this embeded EXIF data yourself (right click the image and choose Properties). Note: I have replaced one of the images, because I could not find the original with the EXIF data embeded anymore.
Visible Area of Earth from 400 km ISS Altitude
Gleem: it should show a flat horizon silly..
No it should not, silly. Did you ever make a calculation or at least a scale model? No, of course not because it could show that you are wrong.
From an altitude of 400 km you see the horizon circle with a radius of 2200 km from above. So no, a circle of radius 2200 km viewed from 400 km above looks not flat, as my Curvature App shows. Note that the radius of the horizon circle is about 1/3 of the radius of the earth. You can really only see a circular section of about 3% of the surface of the earth:
| (4) | |
| (5) | |
| (6) |
Gleem: You have literally just matched a GoPro fisheye to the curve of the earth
No I did not. I downloaded the original image from the NASA website, assuring that they were not taken with a fisheye lens, loaded it unaltered into the Curvature App, entered the altitude of the ISS and the focal length of the camera lens as listed in the embeded EXIF data, rotated and moved the calculated grid as is so that it meets the horizon of the image.
The prediction of the Globe Earth Model from my Curvature App matches exactly what is photographed from the ISS. No deceitful manipulation done.
And of course you ignore all other examples shown on this page, which you can go and observe yourself.
This entire webpage is guilty of the Petitio Principii fallacy. Every single "Globe Model Prediction" uses math which assumes the earth's radius is 6371 km. Don't believe me? Check this link: http://walter.bislins.ch/
Now click on the "Refraction" tab. What do you see? Radius R'=6371
Image: https://i.postimg.cc/
That's right, Petitio Principii fallacy. You're using a sphere earth to prove a sphere earth. Why didn't you compute Terrestrial Refraction in your "Flat Earth Model" predictions? Certainly a Flat Earth has an atmosphere (or atmo-halfsphere).
- When I click "Globe model", I see: Refraction k = 0.250 (medium) with a Temperature Gradient of dT/dh = 0.00655'C/m.- When I click "Flat Earth Model, there is no terrestrial refraction at all, so you're assuming there is no atmosphere and flat earthers live in a vacuum!
Certainly these errors were made on purpose, to support your preferred view of the world. Einstein did the same exact thing when he invented Length Contraction, Time Dilation, and Mass Increase. It was all to support his preferred view of the world- a heliocentric model.
Obviously you're smart enough to know this, but the radius of a flat earth is 0 and it does have an atmosphere and thus terrestrial refraction.
However, I congratulate you on your Curvature App and your work here- it's very well done. Thank you for proving open source code.
Fellow Physicist,
Ryan Zehm
Simulation of Atmospheric Refraction
Spill The Truth, this is not the assumed radius of the earth. This is the Apparent Radius of the Earth R'. A convenient method to show the effect of refraction on visibility is to consider an increased apparent radius of the earth R'. Under this model the light rays can be considered straight lines on an earth of increased radius.
And of course I have to use a radius of 6371 km for the globe model. What else? I want to predict how scenes look like on this planet to compare it with observations. We do not have to prove the earth is a globe, we can download images of the earth from space, directly from the satellites if you don't trust any space agency. But you can make the following experiment to "prove" the globe is this size:
Click here and then change the RadiusPlanet parameter. The image and the model prediction can only be matched if you enter a radius of about 6371 km, which is evidence that the earth is a globe about this big. You can not make the flat earth model match any image, so the flat earth model is falsified, if we assume the known properties of light and atmospheric refraction, which we do exactly.
The reason why I do not simulate refraction on the flat earth model is simply a geometrically restriction of the model. I would have to produce a concave earth. But anyway. Refraction on a flat earth can not produce images which show curvature as observed. Refraction can lessen or exaggerate the curvature of the earth, but not produce this amount of curvature on the flat earth.
If you want a much more realistic simulation of atmospheric refraction on both models, use my App:
This simulation shows that to produce the pictures we can observe, with refraction, on the FE, you would need a temperature gradient of about -15°C per 100 m all the way up to space, which is physically impossible. Click the blue demo button FE Curved to see this simulation. Use the Intro button for a quick intro to the App.
Theory of Relativity is not an Invention of Einstein
Certainly these errors were made on purpose, to support your preferred view of the world.
So you call me a deceiver? Did I hide anything? Did I fake the images? You can go to this locations yourself and make the observations. Before you don't do that, be careful what you call me. And if you are not satisflied with my simulation, make your own and show me how observations match flat earth predictions. You may even use my code as a starting point to save work. Good luck.
Einstein did the same exact thing when he invented Length Contraction, Time Dilation, and Mass Increase. It was all to support his preferred view of the world- a heliocentric model.
First of all, the theory of relativity has nothing to do with the heliocentric model at all. It is an accurate description of some observed properties of nature.
Second, Einstein did not invent relativity. He only was the first person who found a single solution to many yet unexplainable and apparently contradicting observations. The theory is based on and describes observations. Time dilation, length contraction, mass increase, invariance of the speed of light, bending of light and time dilation due to gravity, ect. are observed facts! Electromagnetism would not exist, and as a consequence no atoms would exist, if the theory of special relativity was not right. Today we have so many application that would not exist if we would not have discovered the laws of nature the theory of relativity describes.
- Derivation of Special Relativity from basic observable Principles, written by myself
- Modern applications of special relativity
- Tests of special relativity
- Tests of general relativity
However, I congratulate you on your Curvature App and your work here- it's very well done. Thank you for proving open source code.
Thank you.
Fellow Physicist, Ryan Zehm
Physicist? really?
Regarding the Theory of Relativity I'd also recommend the following link:
https://johanw.home.xs4all.nl/
...and so called "Chronometric Leveling", a rather modern surveying method based on measurements of Gravitational Redshift as per the Theory of Relativity.
Herzlichen Glückwunsch zu dieser ausgezeichneten Internetseite! Ich wünschte, es gäbe einen Award für Dich. Fast alle Flat-Earth-Debunker-Kanäle auf Youtube berufen sich auf Dich und Deine hervorragende Arbeit. Du nimmst sogar den Flat-Earthern die Arbeit ab, ein eigenes Modell zu entwickeln (personal atmospheric dome), und die haben das anscheinend gestohlen *) und es zu ihrer eigenen Erfindung gemacht, ohne zu merken, dass es nur für einige Beobachtungen und unter haarsträubenden Annahmen über die Physik der Lichtbeugung und -brechung funktionieren würde.
Du hast meine Hochachtung.
Beste Grüße
Roland
- ) Ich beziehe mich hier auf ein Video auf Youtube mit dem Titel "Flat Earth Jeran & His Little Secret - One More Nail in the Intellectual Frauds Coffin" (etwa bei 7:20 min), das ich leider nicht verlinken kann.
Danach hat Jeranism "seine Idee" eines atmospheric dome zum ersten Mal vorgebracht, kurz nachdem Du Dein Modell vorgestellt hast.
"This entire webpage is guilty of the Petitio Principii fallacy. Every single "Globe Model Prediction" uses math which assumes the earth's radius is 6371 km"
It's not an assumption. It's a measurable fact. It's also not Petitio Principii if you make predictions based on a model and find that they match reality. If the Earth were not a sphere of radius 6371 km, then reality would not match the predictions of the model, and the model would be falsified. It's perfectly non-circular deductive reasoning. Peititio Principii is much better demonstrated in Flat Earth reasoning, e.g. "all photos of Earth from space are all fake because I know the Earth is flat, therefore all photos of Earth from space are fake".
Citing logical fallacies in Latin is only impressive if you actually know what they mean.
Great Work!
Feel free to use any of the observations on my other channel
Example:
https://www.youtube.com/
https://www.youtube.com/
https://www.youtube.com/
etc...
Sehr schöne Seite, saubere Darstellungen und klare Fakten!
Herzlichen Dank für Ihre Arbeit und beste Grüsse.
I call atmospheric refraction Flat Earthers best friend. It gives them the impression that you can plainly see something that shouldn’t be visible because of earth’s curvature. Could you set up simulations to show how far objects that appear visible because of atmospheric refraction would actually appear if not for refraction
Calculating Distance to just visible Target
David, if you have a target (eg. a mountain) with height hT and the observer's eye height is hO, you can calclulate the distance d so that the target is just fully hidden with the following approximation equation:
| (7) |
| |||||||||||||
| for |
| |||||||||||||
| where' |
| |||||||||||||
As long as the heights are much smaller than the radius of the earth, this approximation is very accurate, at least 3 decimal places accurate if observer and target height are less than 6000 m.
The same equations can be used to calculate the distance with and without refraction. You simply have to choose the corresponding value for R. Because under standard refraction the earth looks less curved, you can use a bigger radius for the earth than it is in reality. For standard refraction 7/6 · Rearth use R = 7433 km. For standard refraction k = 0.17 use R = 7681 km.
There are multiple slightly different values for standard refraction in use. Near the ground the bigger value is more accurate. For higher altitudes the smaller value is more accurate. If you press the button Std the Advanced Earth Curvature Calculator calculates refraction depending on the observer altitude. Near sea level refraction is about k = 0.17.
If you want to know how heigh the observer has to climb to just see the top of the target, use the following approximation:
| (8) |
| |||||||||||||
| for |
| |||||||||||||
| where' |
| |||||||||||||
Note: for observer and target height much less than the radius of the earth, the line of sight distance and the surface distance are identical for all practical purposes. So the equations above hold for both cases.
You can also use my Advanced Earth Curvature Calculator to interactively setup a scene and get the values from it.
Would you please put more images on this page to compare them with flat and globe earth models?
What is the luminous halo which seen above the some of earth pictures taken from ISS?
Aurora
Amir, from time to time I include more examples on this page. Do you have any suggestions?
I'm not sure what you mean by luminous halo. Is it something like in this picture?
This is the Aurora, also called polar lights, northern lights (aurora borealis), southern lights (aurora australis).
"Auroras are produced when the magnetosphere is sufficiently disturbed by the solar wind that the trajectories of charged particles in both solar wind and magnetospheric plasma, mainly in the form of electrons and protons, precipitate them into the upper atmosphere (thermosphere/exosphere) due to Earth's magnetic field, where their energy is lost. The resulting ionization and excitation of atmospheric constituents emits light of varying color and complexity. The form of the aurora, occurring within bands around both polar regions, is also dependent on the amount of acceleration imparted to the precipitating particles."
Source: Wikipedia
No sir. Please look at the first picture of earth from the left on this page. A dim luminous halo is seen above the earth. What is it?
Airglow
Amir, oh, I did not notice that.
This is called Airglow. It's caused by the recombination of ionized atoms (plasma) with free electrons in the Ionosphere. The greenish color is from the recombination of ionized oxigen with electrons in about 100 km altitude.
https://www.universetoday.com/112237/how-to-see-airglow-the-green-sheen-of-night/
https://www.quora.com/What-is-the-band-of-green-light-in-this-picture-taken-from-the-ISS-picture-in-the-description
http://www.miguelclaro.com/wp/?portfolio_category=azores-nightsky
https://www.google.ch/search?newwindow=1$@ffsafe=off$@ffbiw=1368$@ffbih=718$@fftbm=isch$@ffsa=1$@ffei=gsWkXPP_Nb-H1fAP5ZmM-A8$@ffq=airglow+from+ISS$@ffoq=airglow+from+ISS$@ffgs_l=img.3...4401598.4405135..4405456...0.0..0.283.2986.0j10j6....2..1....1..gws-wiz-img.......35i39j0i19j0i5i30i19._BSm1S8UhV4
I would say that all GPS navigation systems, to calculate location effectively, must use a mathematical model based on either a flat earth or a globe. I'll leave it to the reader to guess which one is actually incorporated into the software...
How GPS works
Bill, I assume you know the earth is a globe. But I want to give some infos about GPS anyway.
Actually on the heart of GPS it works in Earth Centered Earth Fixes (ECEF) cartesian coordinates. This is a coordinate system with the origin at the center of the earth, the X axes pointing to the 0-Meridian at the equator, the Y axes pointing to 90° east at the equator and the Z axes pointing up to the north pole. The coordinate system rotates with the earth.
All satellite positions are given in so called Kepplerian parameters, which describe the orbits of each satellite. GPS receivers calculate from this parameters the current locations of all satellites in view in ECEF coordinates. From at least 4 satellite positions in ECEF coordinates and the travel times of the signals from this satellites to the receiver, the location of the receiver is calculated in ECEF coordinates by Multilateration.
So the positions calculated by GPS receivers are independent of the shape of the earth. They work for locations in space as well as for locations on earth. GPS is also used by some space probes and satellites to measure their positions in space. The ISS uses GPS to determine its position and its orientation. The method of Differential GPS is used during rendezvous to determine the range between the ISS and the visiting vehicle. (source Quora).
Only for navigational purposes on earth this coordinates are converted to latitude, longitude and ellipsoid height. The ellipsoid height is further converted into elevation above mean sea level using the Geoid model (Earth Gravity Model 1996, EGM96). The ellispoid coordinates are equivalent to the ECEF coordintes. They describe exactly the same locations in space. You can transform back and forth between this coordinate systems.
If you measure many points on the surface of the earth in ECEF coordinates and plot these points in a 3D application, you get the real shape of the earth, which happens to be a sphere, not a plane. Of course, because otherwise we would not even have the GPS satellites orbiting the earth.
The ellipsoid coordinate system is chosen because the earth is approximately an ellipsoid. If the earth were flat, a cylindrical coordinate system would be more appropriate. If you are at the north pole, the position in ECEF coordinates is (0, 0, 6,356,752.314 + your height). This is equivalent to latitude = 90°, longitude = 0° and h = your height. If you would use cylindrical coordinates for the flat earth, your coordinates would be: latitude = 90°, longitude = 0°, height = greater than 6,356,752.314 m.
Here is a plot of a flight around the earth given as ECEF cartesian coordinates. All points lie on tracks at the altidude of the airplane above a 3D globe. No globe assumed for any calculations. This are the raw 3D data calculated by the GPS receiver. If the earth were flat, all points would lie on a plane, not a globe.
Note: all 18,857 3D coordinates are listed in the table at the end of the linked App. Raw ECEF cartesian coordinates, no latitude, longitude, no globe model assumed.
You can measure the radius of the earth in this App by selecting any 3 points on the same altitude as shown in this picture.
https://youtu.be/MzDuS52o4wc?list=PLGvhNIiu1ubyEOJga50LJMzVXtbUq6CPo$@fft=108
https://www.youtube.com/playlist?list=PLGvhNIiu1ubyEOJga50LJMzVXtbUq6CPo
http://www.navcen.uscg.gov/pubs/gps/gpsuser/gpsuser.pdf
There are no words to describe how grateful I feel about you sharing your work in public. Direct comparison of real world observations with the mathematical models deduced by well established modern theories is priceless and contributes to everybody's better understanding of the world we live in, so a big thank you from me sir.
Unfortunately I found the link to your blog via flat earth debunking videos on YouTube which means I have flushed a fare amount of time in this sink... Although scientific analysis of even the most fundamental level is enough to falsify the flat earth model, delusional people seem to need some "real observable facts" because physics and astronomy to them is merely "unprovable theories comparable to religion". Thus, I would like to contribute some points to this endless discussion from the land surveyor's point of view just to redeem myself for the amount of wasted time:
Regarding Global Navigation Satelite Systems (GNSS). USA, Russia, EU and China all have their own GNSS (GPS, Glonass, Galileo and Beidou respectively), so it's not only the GPS. Using any GNSS receiver (even the ones on smartphones) one can observe the location and orbital movement of the satelites that the receiver gets the signal from in real time. A surveyor's GNSS receiver even displays the satelites of all the aforementioned GNSS (except for Beidou, at least until 2020), not just the GPS. One can also compare the information from different receiver manufacturers and/or mobile application developers to verify it's validity. This is observable using any receiver even without internet connection (so the receiver does not receive faked data through any kind of network). The firmware of the receiver cannot be blamed either because if you go underground (for example in a tunnel) all signal is lost. This "real observable fact" suggests that satelites do exist and are orbiting our skies because their signal on the receiver cannot be faked by any means.
GNSS satelites in orbit move at a considerable speed. In fact, their speed is such that relativistic effects take place and their clocks need to be constantly corrected to "earth time" in order for our measurements to be accurate using high precision atomic clocks. Thus, the accuracy of the measured 3D coordinates that can be achieved on the ground using defferential GPS is constantly in the range of 1-3cm. This is also an observable fact on every surveying GNSS receiver and further reinforces the validity of Special Relativity (SR) equations because if SR was incorrect our satelites would go out of sync and our measured 3D coordinates would become more inaccurate as time goes by, rendering them useless.
GNSS receivers calculate our coordinates in 3D space. All GNSS receivers use ellipsoids as the reference surface upon which calculations are made achieving the afforementioned accuracy. This is an observable fact on all receivers, even on simple mobile applications. Moreover, of these coordinates, the calculation of elevation is of special interest in this discussion. Usually the elevation is in reference to the average sea level which is an irregular surface. "Irregular" in this context means that we cannot describe this surface with equations because the uneven distribution of mass within and on the surface of the earth results in a shape that is not geometrically "perfect". We call this elevation "Orthometric" height and the surface of reference "Geoid" and although we can't use geometry equations directly on the geoid, we can conduct gravitational measurements (not merely observations) to define it with great accuracy. GNSS receivers use equations to calculate the elevation on an elipsoid which we call "Ellipsoid" or "Geometric" height. This is due to the fact that the ellipsoid is the geometric surface that can be used to best approximate the geoid that we gravitationally measure with great accuracy. The result is that we are capable of knowing the height difference of those surfaces in any givven point on earth with great accuracy and thus deduct the orthometric height from our calculated ellipsoid height with, well, great accuracy (2-3 cm with a differential GPS setup). Conclusion: the earth's surface is not approximated by a plain, gravity is real. Additionally, annual investments of billions (or is it maybe trillions) of dollars in infrastructure worldwide actually depend on the accuracy of our instruments and geodetic calculations, rendering the whole concept of "globe conspiracy against the people" rediculous.
Dimitris Gkaranatsios
Rural and Surveying Engineer MSc.
National Technical Univercity of Athens.
- https://en.wikipedia.org/
wiki/ (on GNSS)Satellite_ navigation - https://en.wikipedia.org/
wiki/ (on GNSS receiver's calculations)GNSS_ positioning_ calculation - https://en.wikipedia.org/
wiki/ (on use of atomic clocks in GPS)Atomic_ clock - https://en.wikipedia.org/
wiki/ (on Geoid)Geoid - https://www.e-education.psu.edu/
geog862/ (on height measurements)node/ 1820 - https://www.e-education.psu.edu/
geog862/ (also on height measurements)node/ 1821
Pic de Finestrelles – Pic Gaspard, 443 km
Another one: https://beyondhorizons.eu/
Thiago, thank you for the link. Some flat earther in the comments of the linked page do not understand how refraction can bring back a hidden mountain into view. Here is an animation that explains this:
http://walter.bislins.ch/
We can calculate how much a mountain (or any object) is lifted by refraction with the following equation:
| (9) |
| ||||||||||||
| where' |
|
Note that the distance to the object is squared. This means that the apparent lift of an object increases with the square of the distance, while its angular size decreses only linear with distance. This explains why the lift of very distant objects can be considerably with respect to their small angular size.
Example: Pic Gaspard has a height of 3867 m and is in a distance of d = 443 km. Without refraction from an observer height of 2820 m, the hidden part is 5046 m, so the whole mountain would be hidden. Lets calculate how much standard refraction k = 0.17 can lift the mountain:
| (10) |
|
The horizon at about 200 km distance is also lifted by a certain amount by refraction, hiding part of the raised mountain.
Detailed calculations show that with standard refraction k = 0.17 only 3598 m are still hidden and 269 m of the mountain are now visible. Increasing refraction to medium k = 0.23 results in 3115 m hidden and 752 m visible.
Refraction is always present in an atmosphere. It turns out that even standard refraction is capable of lifting the mountain into view from behind the curvature.
The fact that most of the mountain is hidden by the horizon proves that the earth is a globe. On the Flat Earth the whole 3867 would be visible, as the Curvature Calculator shows.
I'm sorry, but the lake Pontchartrain image is clearly fake. You can check it out easily using google maps.
Here's a link:
https://www.google.com/
TONU, sorry, but the image of the Causeway is not fake. First of all, you are comparing with the wrong bridge. The lake Pontchartrain has 2 bridges. The Causeway is 5 times longer than the bridge you linked and the Causeway is perfectly straight the whole way. Second of all you can not see the curve with a wide angle lens. You have to look along the bridge from the side and use a high zoom camera, because the curvature is very small. Looking along a supposedly straight object lets see the smallest curves. But that is not enough to see the curvature of the earth. You have also to use a zoom lens because zoom compresses distances at the far end and so enhances the curvature, if there is any in the first place.
30°11'8.88"N 90°7'29.33"W
Coordinates of the Causeway (click to open in Google Maps):
walter.bislins.ch/Causeway
Computer model of the Causeway compared with drone video and multiple images, which show the real images only match the model of a spherical earth
walter.bislins.ch/Curve?demo=Causeway
Animation explaining how we can see the curvature using a zoom lens and how Flat Earth and Globe model look different
walter.bislins.ch/Curve?demo=Curve
Watch also the animation explaining from which altitude we can see curvature left to right
It's the image of Lake Ponchartrain Transmission Line i'm talking about. Clearly photoshopped :(
Images are not Faked
TONU: It's the image of Lake Ponchartrain Transmission Line i'm talking about.
Then why do you give the coordinates of a bridge?
The image of the power lines is a screenshot from an enhanced and stabilized video from Soundly. As the original videos below show, it's not photoshoped at all. You can't photoshop a video. So no fake!
Below are the links to the original videos, and they show exactly the same curvature. You can go to lake Pontchartrain anytime and see the same, if you are not too lazy to proof your claim. But don't forget to take you zoom camera with you, because the curve is only visible at the very far end due to perspective compression and due to Perspective on a Globe.
Lake Pontchartrain Transmission Lines Nikon P900
Original video stabilized
Lake Pontchartrain Transmission Lines Nikon P900
Contrast enhanced version the screenshot was taken from
And a drive by showing the power lines from multiple sides
Playlist with some more video unaltered original video footage from Soundly
Live Videos from the Mariott Hotel of the Causeway
Soundly and 2 other guys went into the Mariott hotel at the 15th flor and made a live hangout of the Causeway bridge. They used 3 different cameras and a telescope, all showing the same curvature, live. You could ask Soundly to do certain things. There is no possibility he and the other guys could fake anything.
And a geodetic surveyor drove with a GNSS receiver over both lanes of the bridge and took 6528 measuring points using differential GPS to cm accuracy. This data is a collection of vectors pointing from the center of the earth to the locations of the receiver. He also measured the location of the hotel room. I imported the dataset and an image from Soundly taken from this hotel room into my 3D App and set the 3D camera of the app to the hotel room data point. And peng. The data and Soundly's image match and both show the same curvature. Soundly's image is even less curved due to refraction. The vectors are not affected by refraction.
Here is the Curve
"Jesse Koslowski joins us to share the results of his GPS waypoint mapping of the Lake Pontchartrain Causeway. We will compare and contrast Walter Bislin's models, Jesse's GPS Waypoints, and My photographs to clearly demonstrate the shape of the Earth and dispel the flat-Earth myth that atmospheric effects cause flat planes to look exactly like a Globe." - Soundly
Dataset and Soundly's image overlayed in my 3D App
Measuring the Radius of the Earth from the Causeway Dataset
Zoom-Drone footage from Causeway showing the bridge vanishing behind the horizon
Alone this images and measurements show the earth is curved, deal with it.
The Rainy Lake Experiment
You may or may not be interested in an advanced Bedford Level Experiment, treating the globe and flat earth model equally. It too shows that it is impossible that the earth is flat:
The Rainy Lake Experiment
The Rainy Lake Experiment was designed to show, how we can figure out the shape of the earth, Flat or a Globe, by observing a clever arrangement of targets over a distance of 10 km, taking terrestrial refraction into account and using modern equipment.
Well done Walter. I must reckon you have a valid point in regards to the HORIZON LINE where the eye meets its height. Definetely, there is some sort of divergence. However, this is not enough proof to discard the rest of Earth surface that is still visible to our Eyes to conclude you live on a Globe.
If you think in that respect you should see nothing in front of you. I mean NOTHING or you would be deluding yourself. Do not make a FOOL of yourself again by whatever small flaw you find out that it´s a sign you live on a ball. Get real.
"Mathematical models are not substitute for real experience" - Nikola Tesla. No matter how many Photomontages you, NASA or any other economic corporation use as fact to convince the public they are real when they are not.
Theories are not proven, no matter how close they approximate the real world, they are just Beggar´s Clothes of Blind Faith to get your eyes off the real picture. If your calculations are just based on numbers that come from theories you will never wake up to the Truth. You will live the rest of your life in total darkness, in a world shrouded by numbers that you have never questioned. I assure you, you will never meet God whatever that is.
Pako, nothing will be enough for you to accept the fact that the earth is a globe.
No scientist claims math models ARE reality or scientific theories can prove something. But both are neccessary to make use of nature to our benefit. You are using a device right now that would not exist without the correct math and theories.
Thanks again.
You mean Math models and Theories are necessary to make use of more 'Lies' and to keep on making more Money while we accelerate our own Destruction and deplete nature of its valuable resources for future generations. Break that Balance between true man's needs and Nature abilities to regenerate itself and soon nobody will be left to tell our true but sad story.
By the way have you ever read one of your folks' books? His Name is Viktor Schauberger. My favourite is 'Nature as Teacher'. I bet you are only interested in your own stuff fed by the powers in charge and care not what others can contribute to highlight the true direction man is taking to annihilate himself. Because I´ve already given you links through previous comments and you have not bothered to have a look.
All Photographies are Photoshopped with an exagerated Horizon Eye View to meet a Monetary AGENDA from someone that pays good MONEY to deceive our conception of the Real World. Therefore, all are FAKE IMAGES !!
I only believe what my eyes see, and what my eyes see is that straight objects do not bend nor curve with the distance, they just coincide into a point over our infinitum Horizon Eye View.
Pako, why are you still here if you think all this people are deceiving you? Go somewhere else. Find a satisfying hobby. Nobody is interested in deceiving you. You are not that important.