WaBis
walter.bislins.ch
Finding the curvature of the Earth
- Curvature App stand-alone
- Link to here: walter.bislins.ch/Curve
- German Version
- Causeway Demo: walter.bislins.ch/Causeway
Curvature App: Simulation of Globe-Earth and Flat-Earth
The blue grid in the following Curvature App shows the curvature of the earth at a certain altitude as it appears at a certain Angle of view. The Angle of View, or Field of View (FoV), can also be set as a 35 mm focal length.
- Curve
- Causew
- Soundly
- TrnsmLine
- Rainy
- Tensas
- Grace
- Chicago
- Canigou
- Bedford
- Custom
- Reset
Click a Button to Start a Demo. Click again to skip one step. Click the Animation to start/stop. See also Controls below.
- Views
- Objects 1
- Objects 2
- Refraction
- Units
- Save/Restore
- <<
- Play
- >>
- 0
Please read the paragraph on Refraction to get familiar with this panel.
Use this Formular to convert between different lengh units. You can Copy/Paste the results into input fields in the other Forms.
Get App State Get App Url Set App State Compact Clear
Use this panel to save a certain App state by Get App State and use Copy/Paste to save the state in an external text file. Use Copy/Paste to copy a saved state from an external text file into this panel and click Set App State to activate this state. You can change the Parameters in this panel and apply them by pressing the RETURN button on the keyboard.
Use Get App Url to get an URL containing the current App State. Click Set App State oder copy the URL into any browser address field to go to this page and display the current App State.
Perspective on a Globe
if you have trouble understanding how perspective works on a Globe.
Comparison of Globe and Flat-Earth Model Predictions with Reality
to see a side by side comparison of the model predictions with the corresponding real images.
Lift Data Values
If you activate the option Show Data then there will be 3 Lift values displayed for an object: Absolute Lift of the nearest Object, Lift of the Horizon and Lift of the Object relative to the Horizon. The Lift values express the change in a scene due to Refraction. The values are measures as they appear at the distance of the nearest object in the scene. So if the Horizon Lift is 10 m, that means that the horizon appears to be lifted by 10 m as displayed on a measuring rod at the position of the nearest object.
The Lift values are computed from viewing angles to the base of the nearest object and the horizon line for the cases of zero Refraction and the Refraction entered in Refraction Coeff. k. These angles are then projected onto the plane a the distance from the observer eye to the base of the object in such a way, that if the object is a measuring rod, the lift values can be read from the measuring rod.
If you are looking from above onto a M-Rod object, so that it looks compressed in the vertical direction, the lift values are computed accordingly so the compressed rod can still be used to measure this values. So if a lift value is 5 m and a 10 m rod appears compressed to half its size, you can still use this compressed rod to measure the 5 m, although the lift value as it appears on a measuring rod at the position of the object on a plane perpendicular to the line of sight would only be 2.5 m.
A Lift value always corresponds to the value as read from the (compressed) scale of a M-Rod object at the position of the nearest object.
Views Panel
The simulation parameters are grouped into the panels Views, Objects 1, Objects 2, and Refraction.
 How to use URL parameters to control the App
How to use URL parameters to control the App
In the Views Panel you can choose between the Globe Model, the Flat Earth Model or a side by side view of both.
Earth Model
The Curvature App can be used to compare a spherical earth (Globe) with the Flat-Earth. You can select the desired model with the radio buttons labeled Model:
- Globe shows the scenes as they appear on the globe
- FE shows the scenes as they would look like on a flat earth
- G+FE X shows Globe and Flat Earth side by side, but the Flat Earth is mirrored
- G+FE || shows Globe and Flat Earth side by side, where the models blend into each other
Additional View Parameters
For comparison with the Flat-Earth model, a red grid can be displayed with the Grid setting Projected. The red grid shows the projection of the blue grid onto the plane of the Flat-Earth. For low altitudes, the deviations between the blue ball grid and the red flat grid are minimal. So small indeed that by turning off the red grid the curvature can barely be noticed.
Note that the globe grid does not have a constant spacing. Instead, a certain number of grid lines are displayed, adjustable with the parameter Lines. This corresponds to the natural seeing, because on the earth we have no fixed grid which shows the relative distances either. As a result the distance between the grid lines varies with the distance to the Globe-Earth horizon. The actual distance between the lines is displayed at GridSpacing under Computed Values.
You can choose with CameraAim which point the camera is aiming (Globe Horizon or Flat-Earth Equator FE-Eq) or which reference line (Betwn: line between Globe-Horizon and FE-Equator, or Eye-Lvl) should stay at the center of the graphic, if Tilt = 0.
Zoom, Diag FOV: Zoom factor f (focal length in 35 mm equivalent units) or diagonal Field of View (FOV) in degrees can be used to magnify the image. This two parameters are linked by the following equations (see Angle of view):
| (1) | ||||||||||
| (2) | ||||||||||
| with | ||||||||||
| where' |
|
The Diag FOV is measured diagonally not horizontally. If we assume a 3:2 aspect ratio we can use a conversion factor of c = 1.20185 to convert between diagonal and horizontal FOV. So if you want a horizontal FOV of 60° in the App, you have to enter
- Diag FOV = c · 60° = 1.20185 · 60° = 72.111°.
You can enter a Diag FOV between 0.1° and 160° or a focal length f between 3.81 mm and 24,800 mm. The range of the sliders is narrower.
Eye-Level shows a line at infinity that is the distance Height obove the Flat-Earth plane at the observer. So this line is at the height of the eye of the observer.
Tangent shows the tangent line to the Globe horizon. This is handy to recognize small curvatures of the horizon.
Data displays diverse computed values on the graphics.
Objects Panels
There are two identical-looking Object Panels. You can combine two different sets of objects in a simulation scene. Some objects of the same type may look different in the two panels, e.g. the T-Tower. Use Panel Objects 1 for object in the foreground, and Objects 2 for background objects. The objects can not be mixed in the distance because the drawing algorithm combines all the objects of a group. The representation of mixed objects is optically incorrect.
To display objects in the graphic, a value greater than 0 must be set at NObjects. The type of the object is selected in the lower area of the panel with ObjType. If then no object is visible, it is probably outside the visual range. Change the view area in the Views panel or move the objects with the other parameters in this panel into the view area.
Most of the parameters in this tab are self-explanatory. Note that rows with the same background color are related to each other. With the SideVar radio buttons you can select the mode for lateral movement of the objects, and the slider SideVar can be used to set the magnitude of the displacement. The same applies to SizeVar.
Refraction Panel
All Refraction settings are made in this panel. For a detailed description, see Refraction.
Units-Calculator Panel
Here you can convert lengths into different units. Once a value is entered into a field, all other units are calculated. You can copy a value from one of these fields by copy/paste to a field in another panel. Press the Esc key (applies to all fields of all panels) to reset the field.
Computed Values Panel
The data displayed by these fields can be looked up on the graphics displayed below the panel. The data not specified there are:
AngDiameter (angular diameter) is the angular measurement describing how large the Globe-Earth appears from the distance Height.
GridSpacing is the grid spacing of the blue grid of the globe representation. The distance can be specified in the Views panel with the Lines option.
FrameWidth specifies the horizontal distance between the black frame at the distance of the horizon. If the horizon is not curved and not rotated, this corresponds to the length of the horizon lying within the black frame. The calculation of the length of the effectively visible curved horizon line is too complicated to be packaged into a formula. But this value can be used as a good guess.
HorLftRgtWidth specifies the horizontal distance between the 2 points where the curved horizon comes close to the border of the frame of the image, indicated by 2 small triangles. The line between the 2 points passes through the earth.
HorLftRgtDrop, HorLftRgtDrop∠ are the apparent drop height and angle respectively from the horizon tangent to the line between the 2 points where the curved horizon comes close to the border of the frame, indicated by 2 small triangles. The drop height is calculated from the drop angle using the distance to the center of the horizon HorDistView v. It es an arc with center at the observers eye and the radius is the line of sight to the center of the horizon line.
For a derivation of how HorLftRgt values are calculated see Calculating left-right Horizon Drop.
Refraction
The Curvature App can simulate how Refraction affects the Globe Model. For this purpose, the desired Refraction can be adjusted in the Panel Refraction with the red slider. If the App applies Refraction, the corresponding value is displayed at the bottom of the graph. A Refraction of zero is not displayed.
Refraction of the App can be set A) by one of the parameters Coeff. k, Factor a, Radius R' or with the red slider. Or Refraction can be computed B) from the atmospheric parameters Pressure Press. P, Temperature Temp. T and Temperature-Gradient dT/dh. In case B), Refraction is calculated as soon as the value in dT/dh is changed.
The parameters P, T and dT/dh can also be taken over from the Std-Atmosphere Barometer at the lower part of the panel by choosing BaroLink other than off. The Barometer calculates the parameters for the Standard-Atmosphere on the basis of the observer's altitude Height h.
Attention: Refraction simulation only makes sense below approx. 40 km altitude. When Refraction is coupled to the Standard-Atmosphere (BaroLink = Std-Atm), Refraction automatically decreases with increasing altitude. However, you can enter any values into the fields, but you may get unrealistic Refractions and/or Temperature-Gradients dT/dh.
What is Refraction?
The density of the atmosphere generally decreases exponentially with increasing altitude. Any density change causes a refraction. If the density change is not abrupt but continuous as in the atmosphere, the light is not refracted but bent, but we call it Refraction anyway. Light is always bent in the direction of the higher density, and in the atmosphere that is usually downwards. This means that objects in the distance appear higher than with a straight line of sight. This effect increases with the distance of the observed object, since the light beam travels a larger distance.
Refraction is not a constant phenomenon. It depends strongly on the current atmospheric conditions along the light path and therefore fluctuates on the way to the observer. Since it is impossible to measure the actual refraction from the object to the observer, an average value is obtained which can be calculated from the atmospheric conditions at the observer's location, at least for shorter distances of only some km. But these values can be used for longer distances too, if there are similar conditions along the light path. Above the ground layer refraction does not vary much as shown in Refraction Coefficient as a Function of Altitude. The average value corresponds to a light beam following an arc with the constant radius RR.
Further usefull readings with explanations and simulations of refractions:
- Atmospheric Refraction Phenomena
- Introduction to Superior-Mirage Simulations
- Curvature and Refraction in Surveying and Leveling Through History; Metabunk
- Standard Atmospheric Refraction: Empirical Evidence and Derivation; Metabunk
Refraction-Parameters
Refraction can be expressed by various parameters which depend on each other:
- Refraction-Coefficient k → Coeff. k
- Refraction-Factor a → Factor a
- Apparent Radius of the Earth R' → Radius R'
- Refraction-Angle ρ → ObjRefr∠
The values 1 to 3 are directly linked to each other. As soon as one of these values is specified, the other two are calculated.
Refraction-Coefficient k
The Refraction-Coefficient k is the ratio of the radius of the earth R to the radius of the light ray RR:
| (3) |
|
per definition | |||||||||
| source |
Terrestrial Refraction; Wikipedia | ||||||||||
| where' |
| ||||||||||
If the light ray is not curved, its Radius RR is infinite. This means that for a non-curved light ray the Refraction-Coefficient is k = 0. If the light ray follows the earth's curvature, which is quite possible, then k = 1. The earth appears completely flat in this case.
A standard value of k = 0.13 is often used in the survey. Another frequently used value assumes a light ray radius of RR = 7 · R, which corresponds to a coefficient of k = 0.143 or a Refraction-Factor a = 7/6. The difference is small: for an altitude determination on a distance of 1000 m the difference is only about 1 mm.
The Refraction-Coefficient can be calculated from the atmospheric conditions as follows (Source: Atmospheric refraction):
| (4) |
| ||||||||||||
| see |
Calculating Refraction Coefficient ( | ||||||||||||
| where' |
|
Or if we know k and want to calculate the temperature gradient we can solve (4) for dT/dh:
If we know the refraction index gradient or refractivity gradient we can calculate the refraction coefficient as follow:
| (6) |
| |||||||||||||||||||||
| see |
Refraction in the Atmosphere ( | |||||||||||||||||||||
| where' |
|
Equation (4) can be derived from equation (6):
- Deriving Equations for Atmospheric Refraction
derivation of (6) from the refraction index gradient as calculated from pressure, temperature and humidity.
For Standard-Atmosphere this results in a maximum value of approx. k = 0.17 which decreases continuously with increasing altitude of the observer and is practically zero at an altitude greater than 40 km.
The Temperature-Gradient, i.e. the Temperature Change with increasing altitude, can fluctuate considerably near the surface. While a decrease of Temperature of 0.65°C per 100 m is established under Standard-Atmosphere to an altitude of 11 km, i.e. dT/dh = −0.0065°C/m, a few meters above the surface very different values can be measured. Correspondingly, Refraction is then very different too.
Over cool water or ice, the Temperature-Gradient dT/dh is often positive in a layer above the surface, i.e. the Temperature in the lowest layer of the atmosphere increases with increasing altitude. Such a condition is called an Inversion. If the temperature gradient is greater than −0.01°C/m, in particular in the case of an Inversion, the air is stable (stabile Inversion). If the temperature gradient is less than −0.01°C/m, which is the case with warm soil over cool air, compensating air flows emerge and the air is fluctuating, unstable.
On an Inversion, the down bending of the light beam is the most extreme and can be so strong that the light beam follows the curvature of the earth: k ≥ 1. In this case, the earth appears flat (k = 1) or even concave (k > 1).
If the Temperature-Gradient is more negative than Standard, that is, dT/dh < −0.0065°C/m, which often is the case over a warm surface with a layer of cool air, the light beam is bent less. Refraction k is then smaller than Standard. In the case of a very strong negative Gradient, when the ground is hot, the light beam can even be curved upwards, i.e. the Refraction-Coefficient k is then negative. This results in a fatamorgana or mirage, so layers above the surface appear mirrored.
Note that even if the observer is at a higher elevation, where the ground effect at the observer is negligible, the light rays to distant objects can propagate a great distance along a cool surface like the sea, and are accordingly strongly curved. Therefore on observations over the sea, or a large lake, cities, islands, or mountains can appear, which, according to the formulas, which do not take Refraction into account, must be hidden behind the earth's curvature, see Animations Chicago and Canigou.
Refraction Classification
To get a feel for the impact of Refraction, I have assigned the following classification to the values:
| Coefficient k | 0 to 0.12 | 0.12 to 0.18 | 0.18 to 0.38 | 0.38 to 0.58 | 0.58 to 0.78 | 0.78 to 1 |
|---|---|---|---|---|---|---|
| Classification | weak | standard | moderate | strong | severe | extrem |
Correspondingly, I have assigned the following classification to the Temperature-Gradient:
| dT/dh | less than −0.01°C/m | −0.01 to 0°C/m | greater than 0°C/m |
|---|---|---|---|
| Classification | instable Layer | stable Layer | stable Layer; Inversion |
| Comment | warm surface, cold air | cold surface, warm air |
If a nonzero refraction is set, the value k and dT/dh and their classifications are displayed at the bottom of the graph. If Refraction is calculated from the values for Standard-Atmosphere by setting BaroLink = Std-Atm, this is indicated with the classification Standard Atmosphere.
If the surface temperature is colder than the overlying layer of the atmosphere, the air is very stable. Stable layers suppress convection and turbulent mixing of the air and thus retain their structure. In Standard-Atmosphere, the Temperature-Gradient is only −0.0065°C/m. It is therefore weakly stable.
Source: Atmospheric Temperature Profiles
The more positive the Temperature-Gradient, i.e. the colder the surface is compared to the lowest layer of the atmosphere, the greater Refraction. This explains why, in laser experiments over a frozen lake, no curvature of the earth can be detected because the strong Refraction bends the laser light along the earth's curvature.
Linking Refraction to Standard-Atmonsphäre
The Refraction-Coefficient k can be calculated from the empirically found formula (4) from the current atmospheric conditions at the observer.
In the panel Refraction, the values for pressure P, temperature T and Temperature-Gradient dT/dh for the Standard-Atmosphere are displayed. These values are defined up to a height of approx. 85 km, from then they are displayed as NaN.
If you want to use these values to calculate Refraction, you can select the setting Std-Atm with the option BaroLink. Then the barometer values of the standard atmosphere are linked to Refraction calculations. If you want to set a different Temperature-Gradient but want to use Pressure and Temperature of the Standard-Atmosphere, you can use the option T, P. With off the link is deactivated and you can use any values for Temperature and Pressure, even those that make no sense.
For the other BaroLink options, Temperature and Pressure are linked with the Baro values, but a fixed refraction can be selected. The corresponding Temperature-Gradient is then calculated therefrom. Refraction can also be adjusted with the red slider. Note that these settings are useful only in the lower part of the atmosphere up to approx. 20 km, since Refraction decreases in nature with increasing altitude and does not remain constant.
Refraction-Factor a
In order to be able to use the formulas for the calculation of the obscuration of objects by the curvature of the earth also with consideration of Refraction, there is a trick: simply replace the radius of the earth R by an increased apparent radius of the earth R', which can be calculated from the Refraction-Coefficient k. I denote the conversion factor as Refraction-Factor a:
| (7) |
| ||||||
| see |
Refraction Factor, Apparent Radius of Earth ( | ||||||
| where' |
|
A value of a = 7/6 corresponds to Standard Refraction k = 0.14.
Note: in the literature the Refraction-Factor is often denoted as K (big K). To avoid confusion with the Refraction Coefficient k I use a instead of K.
The Refraction-Factor can be calculated from the refraction index gradient or refractivity gradient as follows:
| (8) |
| |||||||||||||||||||||
| where' |
|
Apparent Radius of the Earth R'
A convenient method to analyse the effect of refraction on visibility is to consider an increased apparent radius of the earth R'. Under this model the light rays can be considered straight lines on an earth of increased radius.
| (9) |
| |||||||||
| see |
Refraction Factor, Apparent Radius of Earth ( | |||||||||
| where' |
|
If Refraction k is nonzero, the Curvature-App uses R' instead of the radius of the earth R for the globe model to simulate the optical effect of Refraction.
Note that the apparent radius of the earth R' is not the radius of curvature of the light ray RR. The relationship between the radii is:
| (10) |
| |||||||||
| where' |
|
Converting between Gradients
We can convert between temperature gradients and refractivity gradients with the following equations:
| (11) |
| |||||||||||||||||||||
| (12) |
| |||||||||||||||||||||
| see |
Converting between Gradients ( | |||||||||||||||||||||
| where' |
|
Refraction-Angle ρ
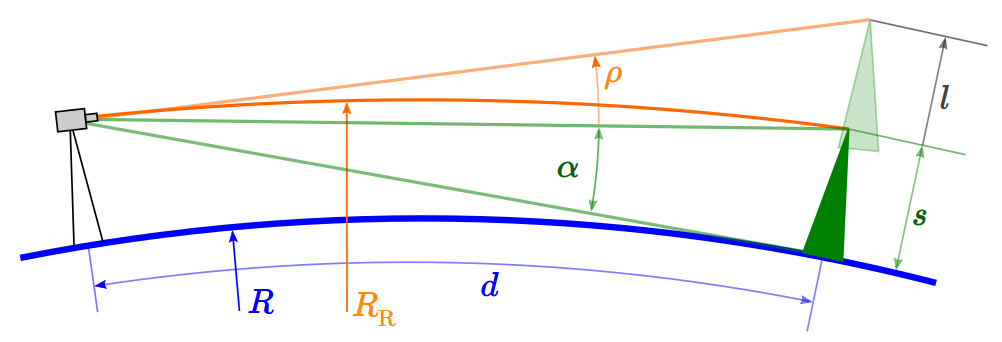
Similarly, as the size of an object can be expressed as an angular size α, the amount an object appears to be raised due to Refraction can be expressed as a Refraction-Angle ρ. The magnitude of the elevation depends on Refraction k and the distance of the object from the observer. The further away an object is, the more it appears raised because the light beam is longer and thus is curved over a longer distance.
The angular size α of an object in degrees is given by its size s and its distance to the observer d. A good approximation for larger distances when d is practically equal to the view distance from the observer to the object is:
| (13) |
| ||||||||||||
| where' |
|
Note: if the distance d of the object is much larger than its size s, the approximation is accurate enough.
The accurate calculation of the Refraction-Angle ρ is complex if we take the slanting of the object into account and is calculated by means of vector geometry. Essentially, the position of the highest point of the nearest object is calculated on a sphere with radius R and on a sphere with radius R'. Then a vector from the observer to each of these two points is calculated. The Refraction-Angle ρ is the angle between these two vectors.
A simpler and good approximation for the Refraction Angle ρ is:
| (14) |
| ||||||||||||
| see |
Refraction Angle and Lift ( | ||||||||||||
| where' |
|
From the Refraction Angle we can calculate the magnitude l of how much an object at distance d appears to be raised due to Refraction:
| (15) |
| |||||||||||||||
| where' |
|
Note: The apparent lift of an object l due to refraction increases with the square of the distance. If the object lies far behind the horizon, the magnitude of its relative raising lrel with respect to the horizon also increases accordingly, although not so strongly, as the nearer horizon also raises with respect to Eye-Level, but to a less extend corresponding to the shorter distance from the observer.
For example, if a mountain is 2000 m high and appears at an angular size of 0.5°, and the Refraction-Angle is 0.25°, the mountain apprears raised an amount of 1000 m. Note that this calculation can be performed without knowing the distance to the object. The distance to the object is contained in the Refraction-Angle. If the mountain is only 1000 m high, its angle size is only half as large: 0.25°. We again obtain the same amount of raising of 1000 m as for the higher mountain, which proves that the raising depends only on the distance, not on the size of the object.
Since the horizon also raises due to Refraction, the raising of an object that lies behind the horizon appears correspondingly less with respect to the horizon. If the object is in front of the horizon, it even lowers with respect to the horizon, although it is raised in absolute terms. This is because the distant horizon appears to be raised more than the object. The greater the distance of the object from the horizon, the greater the relative increase/decrease with respect to the horizon. Very distant Mountains can therefore be raised a considerable proportion of their size beyond the horizon. Thus, Refraction can make mountains, hidden behind the curvature of the earth, visible again to a large extent.
The Refraction-Angle, the angular size and the relative and absolute raising of the object is displayed in the graphic of the App if the option Show: Data on the Views panel is activated. Or they can be read in panel Refraction.
Observations
The earth is huge in comparison to us humans, a diameter of 12,742,000 m compared to human size of 2 m. So huge, indeed, that we are not able to see their spherical shape with the naked eyes from the surface of the earth. We can measure the distance to the horizon and its lowering due to the spherical shape only with precise technical instruments. Only from high altitudes or from space can we clearly see the ball shape of the earth.
Even at altitudes of several kilometers, such as the cruise altitudes of airliners, the spherical shape can not always be clearly identified. A slight curvature can only be detected on wide angle images. It must be taken into account, however, that wide-angle lenses can distort the scene. On cheap cameras or smartphones the curvature can therefore only be observed to a limited extent.
The visibility of the curvature is therefore dependent on the altitude and the angle of view respective the focal length, i.e. zooming!
The fact that the horizon is lower than Eye-Level can not be recognized by the naked eye, since in nature there is no eye-level line above the horizon. However, this drop can be seen with appropriate instruments such as an Overhead Display of an Aircraft.
When zooming in on the horizon along a long straight object like the Causeway Bridge, it looks like the earth is a cylinder. This is due to the  Perspective on a Globe.
Perspective on a Globe.
Superimpose the Grid onto Photos
In order to prove that the calculated blue grid actually reflects reality correctly, the grid can be matched with a real photo.
To superimpose a grid onto a real photo the right way, the following information is required:
- Altitude in which the photo of the earth was taken
- 35mm Focal Length or Angle of view used on taking the image
- Aspect ratio of the image
- The lens must not be distorting, fish-eye lenses are excluded or a Lens Correction must be applied, which removes the distortion.
Use particularly shootings from high altitudes, for example from an airplane or from space. At lower altitudes, no curvature is clearly visible.
Procedure:
Set the altitude with the blue slider or enter the value in the Height input field. Select the focal length or the corresponding angle of view with one of the black sliders. Select the aspect ratio of the image at AspectRatio. With the green sliders Tilt and Roll the viewpoint and the banking angle can be adapted to the photo.
Cut out the area inside the black frame with a program like the Sniping Tool from Windows. Open the photo in any image editing program. Place the cut out area of the grid in a new layer above the photo. Scale the grid plane so that the aspect ratio is maintained and the grid layer becomes the same size as the photo. Set the blending mode of the layer to multiply (or something like that). It may be necessary to move the grid layer slightly and rotate it if the settings of Tilt and Roll do not match exactly.
If everything was done correctly, the grid would now match exactly with the image of the earth's surface. The following photographs show how the results can look like:
Pictures taken from the ISS
The International Space Station ISS orbits the earth at an altitude of 400 km. From this altitude, the earth clearly shows itself as a sphere. I now wanted to check if the calculated grids match with photos taken from the ISS. For this I searched original photos, in which data about the camera and lens used is stored in the images in the EXIF-Format. The reason is, in order to get the correct perspective representation, I have to enter the focal length of the used camera in the Curvature App.
I have found several such images on NASA's website. Below are two such examples with and without superimposed grid:

 Test whether the graphics of the simulation matches a real image taken from the ISS:
Test whether the graphics of the simulation matches a real image taken from the ISS:Height = 400 km; 35mm focal lengt f = 28 mm; Aspect Ratio 3:2; Line Spacing 48.9 km
Date of recording: 16.09.2016 20:55; Source: NASA; Original image with EXIF Informations

 Test whether the graphics of the simulation matches a real image taken from the ISS:
Test whether the graphics of the simulation matches a real image taken from the ISS:Height = 400 km; 35mm focal lengt f = 28 mm; Aspect Ratio 3:2; Line Spacing 48.9 km
Date of recording: 16.09.2016 20:55; Source: NASA; Original image with EXIF Informations
- Swap images
- With Grid
- Without Grid
For the above picture, I used an original photo from NASA. The image was edited according to EXIF data with Photoshop, probably only converted to a JPG. I can't find traces of a composit procedure or any other manipulation and the noise is as expected from a camera with the selected settings.
I have set Height = 400 km and 35mm focal length f = 28 mm in the Curvature App. With Tilt and Roll, I rotated and moved the graphics according to the photo, because the photographer did not aim at the horizon. Then I created a screen copy of the graphics and opened it together with the photo in Photoshop. I have placed the graphics on top of the photo on a new layer and inverted the colors. The graphics and the photo have the same aspect ratio of 3:2. I had to scale the graphics, however, so that it got the same size as the photo. After that, I superimposed the graphics over the photo with blending mode "negative multiply".
And look, the graphics fits exactly to the photo. The lines have a spacing of GridSpacing = 48.91 km. The Gulf of Suez fits exactly between two lines. In Google Earth measured I get about 50 km. So this also fits perfectly.
Below is another picture of the Earth taken from the ISS photographed with the same camera. The superimposed grid of the simulation fits perfectly also here. The faint gray line corresponds to the eye level, i.e. the horizon of a Flat-Earth.

 Another picture of the Earth photographed from the ISS. .
Another picture of the Earth photographed from the ISS. .Height = 400 km; 35mm focal length f = 28 mm; Aspect Ratio 3:2; Line Spacing 147 km
Original image with EXIF Informations

 Another picture of the Earth photographed from the ISS. .
Another picture of the Earth photographed from the ISS. .Height = 400 km; 35mm focal length f = 28 mm; Aspect Ratio 3:2; Line Spacing 147 km
Original image with EXIF Informations
- Swap Images
- With Grid
- Without Grid
Pictures taken from a Rocket Flight
Here are some screen shots taken from the video: GoPro Awards: On a Rocket Launch to Space, which was recorded with a GoPro4 camera with a fish eye lens. I applied the Lens Correction of Adobe Lightroom to it and after that the images fit perfectly to the calculated grid:
Height = 120 km, Focal Length: f = 18 mm, Camera GoPro4
The horizon has exactly the same curvature on all images at every position after applying the Lens Correction.
The Horizon is not at Eye Level
Flat-Earther claim that the horizon is always at eye level, which it would be if the earth were flat. The definition of eye-level is that a line from the eye of the observer to a distant point at the same height forms exactly a 90° angle to the vertical at the observer. The distant horizon of a Flat-Earth would apparently reach to the eye-level and thus form a 90° angle.
A dip-angle from eye-level to the real horizon can not be estimated with the naked eye, since a corresponding reference is missing on the horizon. Just looking straight at the horizon and claiming that it is at eye level, so forms exactly a 90° angle to the vertical, is a false claim. This is true approximately for low altitudes only. In an aircraft at an altitude of 11 km, the horizon drops 3.36° (see DipAngle in the Curvature App). This is a clear drop, but not recognisable with the naked eye because there is no reference.
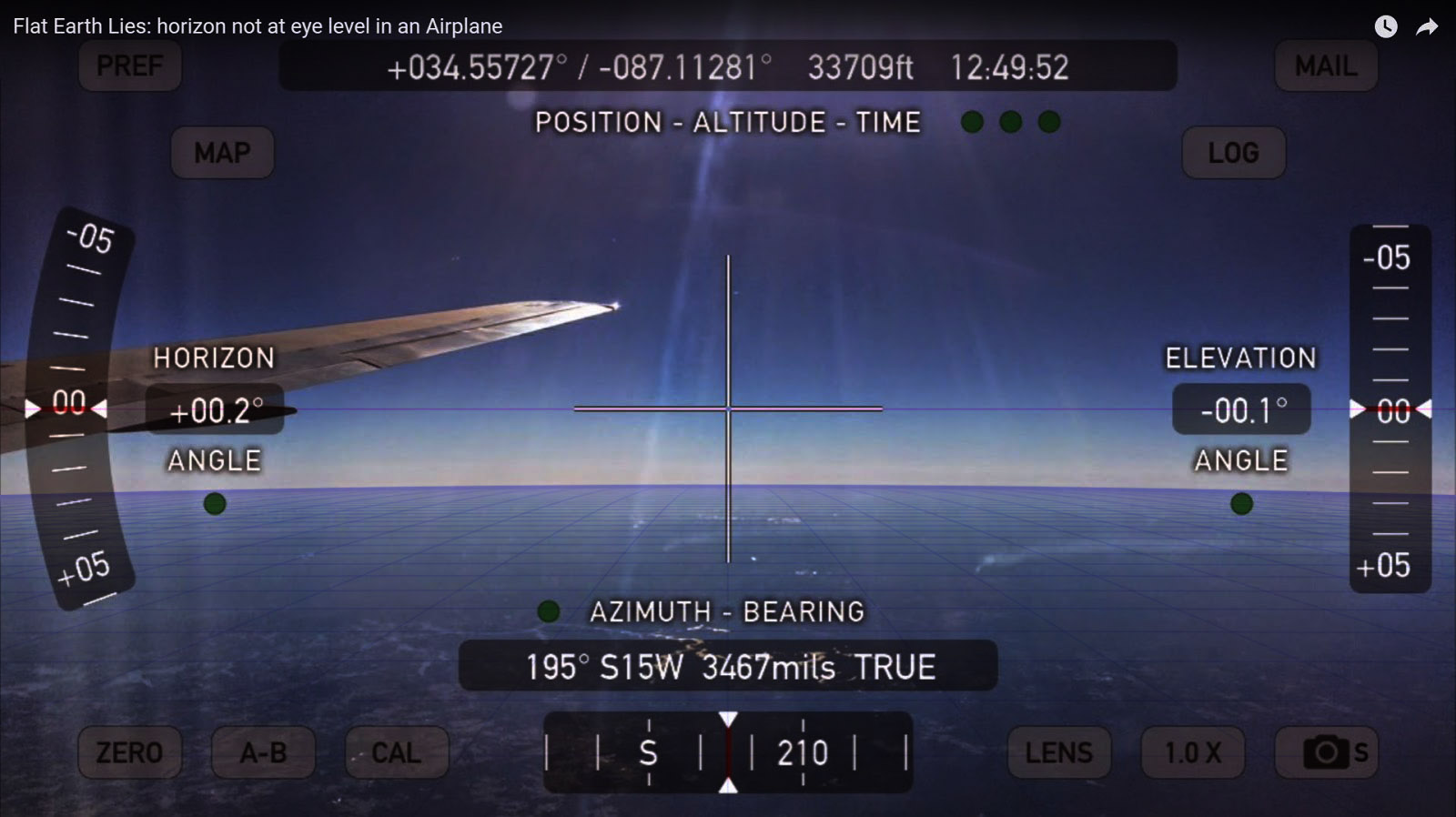
The following photo was taken with the Theodolite App with an iPhone. The aircraft flew at an altitude of 33,709 ft, as noted in the picture at the top/center. The iPhone was aligned so that the crosshair shows eye-level on the horizon. This is the case when the ELEVATION ANGLE shows 0.
 Comparison of the effective horizon line with eye-level in an airplane. .
Comparison of the effective horizon line with eye-level in an airplane. .Height = 10.275 km; 35mm focal lengt f = 33.9 mm; Aspect Ratio: 16:9; GridSpacing 8.035 km; Original Image
 Comparison of the effective horizon line with eye-level in an airplane. .
Comparison of the effective horizon line with eye-level in an airplane. .Height = 10.275 km; 35mm focal lengt f = 33.9 mm; Aspect Ratio: 16:9; GridSpacing 8.035 km; Original Image
- Swap Images
- With Grid
- Without Grid
The calculation results in a dip angle of 3.252°. The horizon is 20.53 km below Eye-Level and is at a distance of 361.6 km. The overlayed grid lines have a spacing of 8.035 km. These values are all calculated by the Curvature App.
I did not take the picture myself but found it at BlogSpot. There is a copy of it on my website. I own the app Theodolite on my iPhone and I know how it works. I calculated the focal length of the iPhone by measuring the angle of view, which I could do with the app. The calculated angle of view of about 65° for the diagonal coincides with data on the Internet. It corresponds to a 35mm focal length of 33.9 mm.
The values: Height = 10,275 km, angle of view 65° and display aspect ratio 16:9 I entered in the simulation. Then I cut out the simulation image along the black frame, scaled it to the same size as the photo and overlayed them with the blending mode multiply. As you can see, the calculated image fits exactly to the photo and shows exactly where the horizon of the Earth is with respect to Eye-Level. Note that a very slight curvature is barely visible on the grid but because of the haze at the horizon not as visible on the photo.
How to observe the horizon drop with a simple home made tool is shown in the following video: Horizon Drop at Varying Altitudes. Flat-Earth Debunked. from madmelon101.
Overhead Displays show Eye-Level

 Rockwell Collins’ Head-up Guidance System (HGS™) incorporates critical flight information into the pilot's field of vision and provides flight path support at all stages of the flight. Source: Rockwell Collins; With kind permission
Rockwell Collins’ Head-up Guidance System (HGS™) incorporates critical flight information into the pilot's field of vision and provides flight path support at all stages of the flight. Source: Rockwell Collins; With kind permissionAirplanes can be equipped with overhead displays. These displays are pushed between the pilot and the front window. When the pilot looks out of the window through this glass screen, he can see all critical flight informations like artificial horizon, speed, altitude, vertical speed, heading, even the runway, and also the terrain like on a night vision device. It is remarkable that the displayed graphics moves in sync with the head movement of the pilot. It looks like the graphics are projected onto the terrain.
If the aircraft is now cruising at high altitudes, in the image at 39,000 ft, the real horizon lies about 3.5° below the eye level due to the earths curvature. The display projects a horizontal line at eye-level into the scene. In the picture you can clearly see the distance between the eye-level line and the real horizon.
The stylized airplane in the display shows the effective flight direction. In the picture, the symbol lies on the horizontal eye-level line, which means that the aircraft neither climbs nor descends. It is located to the left of the center, which means that the aircraft does not fly straight ahead but is pushed sideways to the left from the wind (see arrow on the top left). The aircraft must correct for this deviation by pointing the nose into the wind according the arrow, so that it does not miss the destination. The autopilot automatically performs this correction.
 More evidence the Horizon does not remain at eye level as you gain altitude. for an explanation from a pilot.
More evidence the Horizon does not remain at eye level as you gain altitude. for an explanation from a pilot.




 Deriving Equations for Atmospheric Refraction)
Deriving Equations for Atmospheric Refraction)