This page describes how the measured radius of the earth R3pt in the GNSS Data Viewer and the Geo-Data Visualisation and Calculator App is calculated. The two calculation variants on this page differ by the calculated plane in which the circle given by 3 points is computed. The Geo-Data Visualisation and Calculator App currently only uses the method Plane defined by the Perpendiculars at 2 Points.

Notation: On this page I notate vectors by bold letters like $\mathbf{A} = \vec A$, unit vectors as $\hat {\mathbf{x}} = \mathbf{x} / | \mathbf{x} |$.

Plane through Center of the Earth

Given three 3D points $\mathbf{A}$, $\mathbf{B}$ and $\mathbf{C}$ in cartesian coordinates, find the center $\mathbf{Z}$ and radius $R$ of the circle through this points so that the center of the earth and the points $\mathbf{A}$ and $\mathbf{C}$ lie in the same plane.

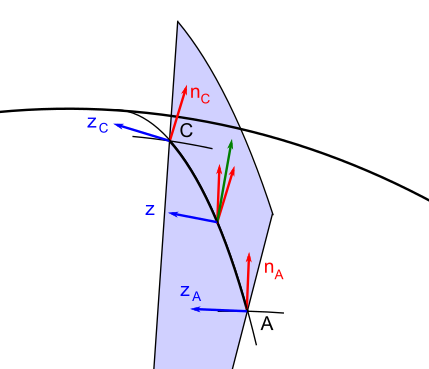
Plane defined by the Perpendiculars at 2 Points

Given three 3D points $\mathbf{A}$, $\mathbf{B}$ and $\mathbf{C}$ in cartesian coordinates, we want to find the center $\mathbf{Z}$ and radius $R$ of the circle through this points so the points $\mathbf{A}$ and $\mathbf{C}$ lie in the same plane. The plane is defined by the normalized vectors $\hat {\mathbf{n}}_\mathrm{A}$ and $\hat {\mathbf{n}}_\mathrm{C}$ that are perpendicular to the ellipsoid at the points $\mathbf{A}$ and $\mathbf{C}$ respectively so that the deviation angle of this normals from the plane is minimal.

In the figure the green vector is the normalized vector sum of $\hat {\mathbf{n}}_\mathrm{A}$ and $\hat {\mathbf{n}}_\mathrm{C}$. The plane normal $\hat {\mathbf{z}}$ (blue vector) is perpendicular to the green vector and the vector from $\mathbf{A}$ to $\mathbf{C}$.

Note: The center of the earth lies normally not on this plane but is nearby.

Problem with 3D Points

To find the center of a circle defined by 3 points, all points must lay on the same plane. The plane is calculated so that the points $\mathbf{A}$ and $\mathbf{C}$ lie on the plane. The middle point $\mathbf{B}$ does not have to be exactly on the plane. It is projected perpendicular to the plane and becomes the 2D point $\mathbf{B}^\prime$.

Most of the calculations are the same for both plane variants. The only difference is how the local coordinate system of the plane is calculated. For the origin of the plane in both variants the point $\mathbf{A}$ is chosen.

a) Plane through the Center of the Earth

First we define the plane by a local coordinate system with the origin at $\mathbf{A}$, X-axes from the center of the earth in the direction to point $\mathbf{A}$, Z-axes perpendicular to the vectors $\mathbf{A}$ and $\mathbf{C}$ and the Y-axes perpendicular to X and Z in a right handed system.

The hat above the variables like $\hat {\mathbf{x}}$ denotes unit vectors. $\mathrm{norm}( \mathbf{A} ) = \mathbf{A} / | \mathbf{A} |$ gives the unit vector in the direction of $\mathbf{A}$ and $\times$ is the vector cross product.

b) Plane defined by the Perpendiculars at 2 Points

First we calculate the perpendicular vector $\hat {\mathbf{z}}$ for the plane as the mean vector of a perpendicular plane vector $\hat {\mathbf{z}}_\mathrm{A}$ at point $\mathbf{A}$ and $\hat {\mathbf{z}}_\mathrm{C}$ at point $\mathbf{C}$. This z-vectors are the cross product of the vector $\mathbf{D}$ from $\mathbf{A}$ to $\mathbf{C}$ and the perpendiculars $\hat {\mathbf{n}}_\mathrm{A}$ and $\hat {\mathbf{n}}_\mathrm{C}$ respectively.

The X-axis direction is then perpendicular to $\hat {\mathbf{z}}$ and $\mathbf{D}$ and the Y-axes perpendicular to $\hat {\mathbf{x}}$ and $\hat {\mathbf{z}}$ in a right handed system.

Lets calculate some intermediate vectors:

Now we can calculate the plane coordinate system:

Common calculations

Now we transform $\mathbf{A}$, $\mathbf{B}$ and $\mathbf{C}$ into this plane 2D coordinate system so that $\mathbf{A}$ is the origin. Note that by this process the vector $\mathbf{B}$ gets automatically projected onto the plane because the Z-component is ignored. The 2D plane coordinates of the points are denoted as $\mathbf{A}^{\prime}$, $\mathbf{B}^{\prime}$ and $\mathbf{C}^{\prime}$:

The center of the circle lies on the two perpendiculars through the middle points between A'-B' and B'-C'. The middle points can be calculated by adding the vectors and scale it by a factor 1/2:

The direction of the perpendiculars through $\mathbf{M}_\mathrm{a}$ and $\mathbf{M}_\mathrm{b}$ can be calculated from the 90° rotated unit vectors from $\mathbf{A}^{\prime}$ to $\mathbf{B}^{\prime}$ and $\mathbf{B}^{\prime}$ to $\mathbf{C}^{\prime}$:

Rotating by 90° counter clockwise using the function $\mathrm{rot}_{90}$ gives:

Now we can describe the equations for the two middle perpendicular lines. The center of the circle is the intersection of the two lines:

Because each vector in the equation (8) has 2 components, we have 2 equations for the unknown factors a and b.

We only need one of this factors to calculate the center of the circle on the plane. We can solve both equations (9) for a and subtract the results. This gives us one equation for the unknown b. Solving for b gives:

We can now insert b into (8) and get the center of the circle in plane coordinates:

The radius of the circle is the length of the vector from $\mathbf{Z}^{\prime}$ to $\mathbf{A}^{\prime}$, $\mathbf{B}^{\prime}$ or $\mathbf{C}^{\prime}$:

The center of the circle in the original 3D coordinate system can be calculated as follows:

JavaScript Code

  CircleFrom3PointsAndNormals: function( A_3d, B_3d, C_3d, NA_3d, NC_3d ) {
    // returns { R: radius, Center: [ x, y, z ] } coords in ECEF
    //
    // if NA_3d and NC_3d are defined, then
    //   the circle plane is such that A and B lie on the plane
    //   and the plane normal is calculated from the ellispoid perpendicular vectors NA_3d, NC_3d
    //   such that the plane lies between this vectors.
    // else
    //   the plane is defined by the points A_3d, B_3d, and the center of the earth

    // calculate plane local coord sys
    var x, y, z;
    if (V3.Ok(NA_3d) && V3.Ok(NC_3d)) {

      // the circle plane is such that A and B lie on the plane
      // and the plane normal is calculated from the ellispoid perpendicular vectors NA_3d, NC_3d
      // such that the plane lies between this vectors.
      // This is due to the fact that this vectors may be angled perpendicular to the connection of A and C
      var D_3d = V3.Norm( V3.Sub( C_3d, A_3d ) );
      var na = V3.Norm( V3.Mult( NA_3d, D_3d ) );
      var nc = V3.Norm( V3.Mult( NC_3d, D_3d ) );
      z = V3.Norm( V3.Add( na, nc ) );
      x = V3.Norm( V3.Mult( D_3d, z ) );
      y = V3.Mult( z, x );

    } else {

      // circle plane contains the center of the earth
      z = V3.Norm( V3.Mult( A_3d, C_3d ) );
      x = V3.Norm( A_3d );
      y = V3.Mult( z, x );

    }

    // transform points into plane coord system
    var B0_3d = V3.Sub( B_3d, A_3d );
    var C0_3d = V3.Sub( C_3d, A_3d );
    var A = [ 0, 0 ];
    var B = [ V3.ScalarProd( B0_3d, x ), V3.ScalarProd( B0_3d, y ) ];
    var C = [ V3.ScalarProd( C0_3d, x ), V3.ScalarProd( C0_3d, y ) ];

    // calculate mid points
    var Ma = V2.Scale( V2.Add( A, B ), 0.5 );
    var Mb = V2.Scale( V2.Add( B, C ), 0.5 );

    // calculate middle perpendicular directions
    var ra = V2.Norm( V2.Sub( B, A ) );
    var rb = V2.Norm( V2.Sub( C, B ) );
    // rotate counter clockwise
    var sa = [ -ra[1], ra[0] ];
    var sb = [ -rb[1], rb[0] ];

    // equations of middle perpendiculars are:
    // Z = Ma + a * sa = Mb + b * sb
    // solve for b (or a)
    var b = (sa[0] * (Mb[1] - Ma[1]) - sa[1] * (Mb[0] - Ma[0])) / (sb[0] * sa[1] - sb[1] * sa[0]);

    // center of circle on plane
    var Z = V2.Add( Mb, V2.Scale( sb, b ) );

    // radius of circle
    var R = V2.Length( V2.Sub( A, Z ) );
    if (b < 0) R *= -1;

    // transform center to 3D
    var Z0_3d = V3.Add( V3.Scale(x, Z[0]), V3.Scale(y, Z[1]) );
    Z_3d = V3.Add( Z0_3d, A_3d );

    return { R: R, Center: Z_3d };
  }