Sudoku: Basic Fish
Als Fish (Fisch) bezeichnet man eine Gruppe von Methoden, die alle das gleiche Prinzip verwenden. Als Basic Fish (einfacher Fisch) bezeichne ich Fische, die nur Zeilen und Spalten betreffen und keine zusätzlichen Komplikationen wie Fins, Finned Fish (Flossen, Fisch mit Flossen) oder Mutationen, Mutant Fish enthalten. Fische findet man nur mit Hilfe des Kandidaten-Gitters. Einfache Fische wie der X-Wing sind leicht zu erkennen, während grössere Fische nur mit Mühe zu entdecken sind.
Diese Seite beschreibt das Prinzip hinter einem Basic Fish und enthält Beispiele für die grösseren Fische. Der X-Wing wird auf einer separaten Seite beschrieben.
Logik des Basic Fishes
Bei der Suche nach einem Fisch konzentriert man sich auf eine bestimmte Zahl im Kandidaten-Gitter. Am besten nimmt man dazu den Filter-Modus zuhilfe.
Wenn N Zeilen existieren, in denen der betrachtete Kandidat nur in genau denselben N verschiedenen Spalten vorkommt, so haben wir einen Fisch gefunden. Die Zeilen nennt man in diesem Fall Base-Set und die Spalten Cover-Set. Die Zellen an den Schnittpunkten der Zeilen und Spalten nenne ich Kreuzungs-Zellen. Es gibt bei einem Fish N mal N solche Kreuzungs-Zellen.
Die Logik ist nun folgende. Jede der N Zeilen (Base-Set) muss genau einen der betrachteten Kandidaten als Lösungs-Zahl enthalten. Aber auch in jeder der N Spalten (Cover-Set) muss jeweils genau einer der Kandidaten eine Lösungs-Zahl sein. Wir wissen zwar noch nicht, in welchen der N mal N Kreuzungs-Zellen der Kandidat jeweils gesetzt werden kann. Da aber in jeder Zeile des Base-Set genau einer der Kandidaten einer Kreuzungs-Zelle gesetzt sein muss, ist auch in der entsprechenden Spalte des Cover-Set derselbe Kandidat gesetzt. In jeder Spalte des Cover-Sets kann also der Kandidate nur in einer der Kreuzungs-Zellen gesetzt sein. Daher können alle Kandidaten aus den Cover-Set Spalten gelöscht werden, die sich nicht in den Kreuzungs-Zellen befinden.
Zu beachten ist, dass der betrachtete Kandidat nicht in jeder der N Kreuzungs-Zellen des Base-Sets vorkommen muss. Aber der Kandidat darf beim Basic Fish nur in den N Kreuzungs-Zellen des Base-Sets vorkommen. In jeder Zeile des Base-Sets müssen aber mindestens 2 Kandidaten vorkommen, sonst hätte die enstprechende Zeile einen Naked Single und man müsste nicht die Fish-Methode auf diese Zeile anwenden.
Dieselbe Beschreibung gilt auch, wenn Zeilen und Spalten vertauscht werden: Wenn N Spalten existieren, in denen der betrachtete Kandidat nur in genau denselben N verschiedenen Zeilen vorkommt, so haben wir einen Fisch gefunden. In diesem Fall nennt man die Spalten Base-Set und die Zeilen Cover-Set. Jede der N Spalten (Base-Set) muss genau einen der betrachteten Kandidaten als Lösungs-Zahl enthalten. Aber auch in jeder der N Zeilen (Cover-Set) muss jeweils genau einer der Kandidaten eine Lösungs-Zahl sein. Da in jeder Spalte des Base-Set genau einer der Kandidaten einer Kreuzungs-Zelle gesetzt sein muss, ist auch in der entsprechenden Zeile des Cover-Set derselbe Kandidat gesetzt. In jeder Zeile des Cover-Sets können also die Kandidaten nur in einer der Kreuzungs-Zellen gesetzt sein. Daher können alle Kandidaten aus den Cover-Set Zeilen gelöscht werden, die sich nicht in den Kreuzungs-Zellen befinden. Zu beachten ist auch hier, dass der betrachtete Kandidat nicht in jeder der N Kreuzungs-Zellen des Base-Sets vorkommen muss.
Fisch-Arten
Die Anzahl an Base-/Cover-Sets bestimmt die Grösse des Fisches und damit seinen Namen. Die folgenden Namen werden verwendet:
| Grösse | Name |
|---|---|
| 2 | X-Wing (Kreuzflügler; ein X-Wing ist ein Fisch und kein Wing!) |
| 3 | Swordfish (Schwertfisch) |
| 4 | Jellyfish (Qualle) |
| 5 | Squirmbag |
| 6 | Whale (Wal) |
| 7 | Leviathan |
Beispiel Swordfish (3-Base Fish)
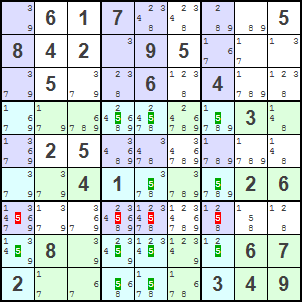
Code: 1(679)85(679)(79)234 5(469)(469)3(469)2178 (247)(2347)(2347)8(147)(147)569 8(124)(124)6(124)5793 (267)(267)59(237)(37)481 3(1479)(179)(14)(147)8652 98(47)2(45)631(57) (2467)(1234567)(123467)(14)(13459)(1349)8(24)(567) (246)(123456)(12346)78(134)9(24)(56) [1]
In diesem Beispiel konzentrieren wir uns auf die 4-er Kandidaten im Kandidaten-Gitter. Wir finden 3 grüne Zeilen (2, 4, 7) in welchen der 4-er Kandidat nur in Kreuzungs-Zellen mit den 3 blauen Spalten (2, 3, 5) vorkommt. Wir haben einen Sword Fish (Schwetfisch), also einen Fisch der Grösse N = 3 gefunden. In Zeile 7 kommt der 4-er Kandidat zwar nicht in allen 3 Spalten des Cover-Set vor, dies ist aber mit der Logik des Basic Fishes konform. Keiner der grün markierten 4-er Kandidaten kommt ausserhalb der hellblauen Kreuzungs-Zellen der günen Zeilen vor. In jeder anderen Zeile kommt entweder kein 4-er Kandidat vor oder die Zeile hat 4-er Kandidaten die nicht in den 3 blauen Spalten liegen.
Logik: In jeder der 3 grünen Zeilen (Base-Set) muss genau einer der grün markierten Kandidaten eine Lösungs-Zahl sein. Aber auch in jeder der 3 Spalten (Cover-Set) muss jeweils genau einer der Kandidaten eine Lösungs-Zahl sein. Wir wissen zwar noch nicht, in welchen der hellblauen Kreuzungs-Zellen der Kandidat jeweils gesetzt werden kann. Da aber in jeder Zeile des Base-Set genau einer der Kandidaten einer Kreuzungs-Zelle gesetzt sein muss, ist auch in der entsprechenden Spalte des Cover-Set derselbe Kandidat gesetzt. In jeder Spalte des Cover-Sets kann also der Kandidaten nur in einer der Kreuzungs-Zellen gesetzt sein. Daher können alle rot markierten Kandidaten aus den Cover-Set Spalten gelöscht werden, die sich nicht in den Kreuzungs-Zellen befinden.
Code: 1(679)85(679)(79)234 5(469)(469)3(469)2178 (247)(2347)(2347)8(147)(147)569 8(124)(124)6(124)5793 (267)(267)59(237)(37)481 3(1479)(179)(14)(147)8652 98(47)2(45)631(57) (2467)(1234567)(123467)(14)(13459)(1349)8(24)(567) (246)(123456)(12346)78(134)9(24)(56) [1]
Dies ist dasselbe Beispiel wie oben. In dieser Konstellation können wir auch einen Sword Fish mit einem Spalten-Base-Set für denselben 4-er Kandidaten finden. Wir finden 3 grüne Spalten (1, 6, 8) in welchen der 4-er Kandidat nur in den Kreuzungs-Zellen mit den 3 blauen Zeilen (3, 8, 9) vorkommt. In Spalte 8 kommt der 4-er Kandidat zwar nicht in allen 3 Zeilen des Cover-Set vor, dies ist aber mit der Logik des Basic Fishes konform. Keiner der grün markierten 4-er Kandidaten kommt ausserhalb der hellblauen Kreuzungs-Zellen der günen Spalten vor. In jeder anderen Spalte kommt entweder kein 4-er Kandidat vor oder die Spalte hat 4-er Kandidaten die nicht in den 3 blauen Zeilen liegen.
Nach der Logik des Basic Fishes können alle rot markierten Kandidaten gelöscht werden. In der gelben Zelle bleibt dabei nur noch der 1-er Kandidat übrig. Im nächsten Schritt kann also in der gelben Zelle die Zahl 1 eingesetzt werden.
Beispiel Jellyfish (4-Base Fish)
In diesem Beispiel zeige ich, wie man mit Hilfe des Filter-Modus auch grössere Fische finden kann. Im Linken Bild ist der Filter-Modus für die 5-er Kandidaten aktiv. Wir sehen, dass in 5 Zeilen und in 5 Spalten gelbe Zellen vorkommen. Der grösste mögliche Fisch ist ein 4-Base Fish (Jellyfish). Wir schauen also, ob es 4 Zeilen gibt, in denen der 5-er Kandidat nur maximal 4 mal vorkommt und dies auch noch in denselben 4 Spalten. Das ist tatsächlich der Fall, nur die Zeile 7 hat 5 gelbe Zellen.
Wir haben also einen Jellyfish gefunden. Im Kandidaten-Gitter rechts mit deaktiviertem Fileter-Modus sieht man den Fisch besser. Die rot markierten 5-er Kandidaten können gelöscht werden.
Beachte, dass in Zeile 7 der letzte 5-er Kandidat in Spalte 8 nicht gelöscht werden kann, weil er in keinem Cover-Set (blaue Spalten) steht (siehe Logik des Basic Fishes).
Hinweis: Da die gelbe Zelle in Zeile 7 Spalte 8 die einzige Zelle mit einem 5-er Kandidaten in der Spalte 8 ist, handelt es sich hier um einen Hidden Single. Wenn in diese Zelle die Zahl 5 gesetzt wird, fallen die rot markierten 5-er auch weg. Man braucht in dieser Konstellation also nicht nach einem grossen Fisch zu suchen.
Beispiel Whale (6-Base Fish)
Hier noch ein Beispiel eines Walfisches (6-Base Fish). Im Linken Bild ist der Filter-Modus für die 8-er Kandidaten aktiv. Wir sehen, dass in 7 Zeilen und in 7 Spalten gelbe Zellen vorkommen. Der grösste mögliche Fisch dieser Konstellation ist ein 6-Base Fish (Wale). Wir schauen also, ob es 6 Zeilen gibt, in denen der 8-er Kandidat nur maximal 6 mal vorkommt und dies auch noch in denselben 6 Spalten. Wir finden 7 Zeilen mit je 6 Kandidaten. Aber Zeile 4 hat einen Ausreisser: die Zelle Zeile 4 Spalte 3 ist die einzige gelbe Zelle in der Spalte 3. Wenn wir die Zeile 4 vom Base-Set ausschliessen, belegen die verbliebenen gelben Zellen insgesamt genau 6 Spalten (Cover-Set).
Wir haben also einen Wale gefunden. Im Kandidaten-Gitter rechts mit deaktiviertem Fileter-Modus sieht man den Fisch besser. Die rot markierten 8-er Kandidaten können gelöscht werden.
Beachte, dass in Zeile 4 der erste 8-er Kandidat in Spalte 3 nicht gelöscht werden kann, weil er in keinem Cover-Set (blaue Spalten) steht (siehe Logik des Basic Fishes).
Hinweis: Da die gelbe Zelle in Zeile 4 Spalte 3 die einzige Zelle mit einem 8-er Kandidaten in der Spalte 3 ist, handelt es sich hier um einen Hidden Single. Wenn in diese Zelle die Zahl 8 gesetzt wird, fallen die rot markierten 8-er auch weg. Man braucht in dieser Konstellation also nicht nach einem grossen Fisch zu suchen.